v_B=1.71 m/s; a_B=3.26 m/s²

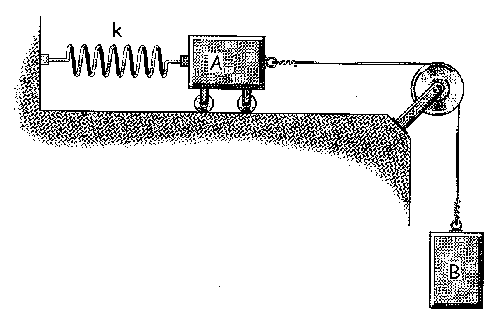
En primer lugar determinamos las masas de los bloques A y B:

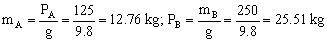
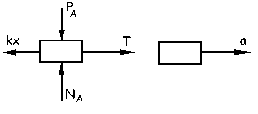Trazamos ahora el diagrama de sólido libre del bloque A. Tomaremos como ejes el eje X horizontal y positivo hacia la derecha y el eje Y vertical y positivo hacia arriba. Este bloque sólo se mueve en la dirección x. Para este bloque:

ΣF_x=ma ⇒ T-kx=m_Aa ⇒ T=m_Aa+kx

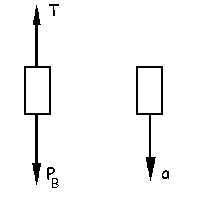
Ahora trazamos el diagrama de sólido libre del bloque B. Tendremos en cuenta que los dos bloques están unidos por una cuerda inextensible, por lo que ambos se moverán con la misma velocidad y aceleración (cuando el resorte se estira una cantidad x, el bloque A se mueve hacia la derecha esa misma cantidad x y el bloque B baja hacia abajo la misma distancia x). Para este segundo bloque:

ΣF_y=m_Ba ⇒ P_B-T=m_Ba ⇒ T=P_B-m_Ba

Igualando las dos expresiones que hemos obtenido para la tensión:

m_Aa+kx=P_B-m_Ba ⇒ 12.76a+417x=250-25.51a ⇒ 38.27a=250-417x ⇒ a=6.53-10.9x

Teniendo en cuenta que la aceleración es la derivada de la velocidad respecto del tiempo:

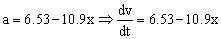
Multiplicamos y dividimos al primer miembro por un elemento diferencia de espacio, dx:

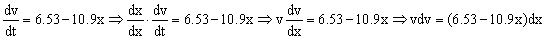
Y como ya tenemos las variables separadas, procedemos a la integración de la ecuación, teniendo en cuenta las condiciones iniciales (cuando t=0 ⇒ x=0 ⇒ v=0) con lo cual nos queda:

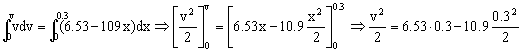
De donde obtenemos:

v=1.71 m/s

Ahora para este valor de x la aceleración valdrá:

a=6.53-10.9x=6.53-10.9 · 0.3=3.26 m/s²

a=3.26 m/s²