r=12.90 m; t=0.674 s

En primer lugar vamos a determinar la velocidad que tendría el paracaidista al llegar al suelo cayendo desde 1 m de altura. El movimiento sería rectilíneo uniformemente acelerado, siendo la aceleración la de la gravedad, luego tendríamos:

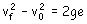
siendo v_f la velocidad final, v₀ la inicial, g la aceleración de la gravedad y e el espacio recorrido. Teniendo en cuenta que el paracaidista partiría del reposo:

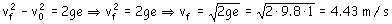
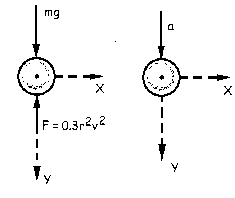Por tanto el paracaidista debe llegar al suelo con una velocidad de 4.43 m/s. Trazamos su diagrama de sólido libre y tendremos lo que aparece en la figura. Para el eje Y:

ΣF_y=ma ⇒ mg-F=ma ⇒ mg-0.3r²v²=ma

A medida que la velocidad aumenta, la fuerza F también aumenta, hasta que es igual al peso y lo contrarresta, de modo que la aceleración es nula y a partir de ese instante el paracaidista cae con velocidad uniforme, y dicha velocidad recibe el nombre de velocidad límite. Por tanto, la velocidad límite que debe alcanzar el paracaidista es de 4.43 m/s. Si en este momento la aceleración es nula:

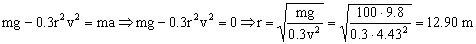
r=12.90 m

Ahora necesitamos la expresión de la velocidad en función del tiempo, para ver cuándo dicha velocidad es de 4 m/s. Teniendo en cuenta que la aceleración es la derivada de la velocidad respecto del tiempo, la ecuación del movimiento nos queda:

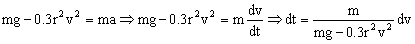
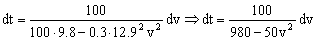
Tenemos las variables separadas, luego podemos integrar, teniendo en cuenta que cuando t=0 ⇒ v=0:

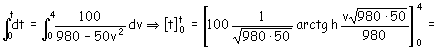
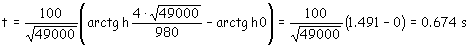
t=0.674 s