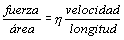R=Cηrv

Tendremos la ecuación:

R=Cη^a r^b v^g

donde C es una constante que supondremos adimensional.

Las dimensiones de cada factor son:

[ R] =MLT^-2

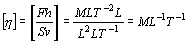
[ r] =L

[ v] =LT^-1

Por tanto tendremos, sustituyendo en la ecuación de dimensiones:

R=Cη ^a r^b v^g ⇒ MLT^-2=(ML^-1T^-1)^a (L)^b (LT^-1)^g ⇒ MLT^-2=M^a L^–aT^–aL^b L^g T^–g  ⇒

MLT^-2=M^a L^{–a +b+ g} T^–a–g

Como las bases son iguales, los exponentes también deben ser iguales, con lo que tendremos las siguientes tres ecuaciones:

1=a

1=-a +b +g

-2=-a –g

De cuya resolución obtenemos:

a =1; b =1; g =1

Con lo cual la ecuación pedida es:

R=Cη^ar^bv^g=Cη rv

R=Cη rv