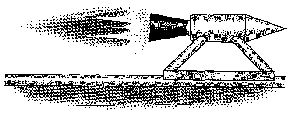Problema de Dinámica de la Partícula

El trineo representado en la figura se utiliza para el ensayo de pequeños cohetes propulsores de combustible sólido. La masa combinada del cohete y el trineo es de 1000 kg. De las características del combustible, se sabe que el empuje que proporciona el cohete durante el movimiento del trineo puede expresarse en la forma:

F=a+bt-ct2

donde F se expresa en N y t en segundos. Si el trineo parte del reposo cuando el empuje del cohete es de 10 kN, recorre 700 m y alcanza una velocidad de 150 m/s durante un recorrido de prueba de 10 s, determinar: a) los valores de las constantes a, b y c; b) las aceleraciones máxima y mínima que experimenta el trineo durante el ensayo. Despreciar la fricción entre el trineo y los raíles y la reducción de masa del combustible durante la prueba.

a) a=10000 N; b=1800 N/s; c=120 N/s2
b) amáx=16.75 m/s2; amín=10 m/s2

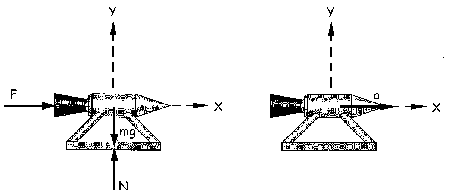
a) En primer lugar realizamos el diagrama de sólido libre del cohete con el trineo y el sistema de referencia que utilizaremos en el problema.

Además, sabemos que cuando t=0 ⇒ F=10000 N, luego sustituyendo esto en la expresión de F obtenemos ya una de las constantes:

F=a+bt-ct2 ⇒ 10000=a

a=10000 N

Y la ecuación de la fuerza nos queda:

F=a+bt-ct2=10000+bt-ct2

Ahora para el eje X tendremos:

ΣFx=ma ⇒ F=ma

Utilizando la expresión que nos da la fuerza F en función del tiempo, y teniendo en cuenta que la aceleración es la derivada de la velocidad respecto del tiempo:

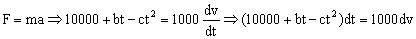
Integramos esta ecuación teniendo en cuenta que cuando t=0 ⇒ v=0:

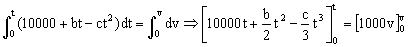
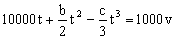
Además, sabemos que el trineo alcanza una velocidad de 150 m/s cuando t=10 s luego:

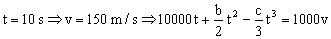
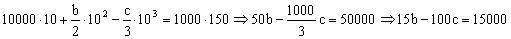
Y ahora podemos tener en cuenta que la velocidad es la derivada del espacio respecto del tiempo, y tendremos:

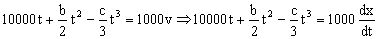
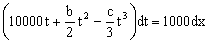
Integramos ahora teniendo en cuenta que cuando t=0 ⇒ x=0:

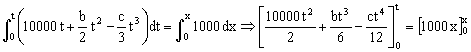
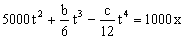
Sabemos que cuando t=10 s ⇒ x=700 m luego nos queda la ecuación:

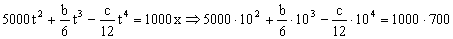
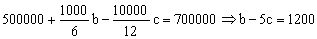
Tenemos un sistema de dos ecuaciones y dos incógnitas, que son:

15b-100c=15000

b-5c=1200

De la segunda ecuación:

b-5c=1200 ⇒ b=5c+1200

Sustituyendo en la primera:

15b-100c=15000 ⇒ 15(5c+1200)-100c=15000 ⇒ 75c+18000-100c=15000 ⇒ 3000=25c

c=120 N/s2

Y la otra constante:

b=5c+1200=5 · 120+1200=1800 N/s

b=1800 N/s

b) La fuerza F, una vez determinadas las tres constantes, vale:

F=a+bt-ct2=10000+1800t-120t2

Para que la aceleración sea máxima o mínima su derivada respecto del tiempo debe ser nula. Tenemos de la expresión obtenida a partir del diagrama de sólido libre:

ΣFx=ma ⇒ F=ma ⇒ 10000+1800t-120t2=1000a ⇒ a=10+1.8t-0.12t2

Derivamos e igualamos a cero:

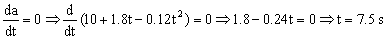
Además, sabremos si es máxima o mínima en función del signo de la segunda derivada:

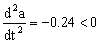
Como la segunda derivada respecto del tiempo es negativa, eso implica que en t=7.5 s la aceleración toma un valor máximo, que será:

a=10+1.8t-0.12t2=10+1.8 · 7.5-0.12 · 7.52=16.75 m/s2

amáx=16.75 m/s2

En los extremos del intervalo tendríamos:

t=0 ⇒ a=10+1.8t-0.12t2=10 m/s2

t=10 s ⇒ a=10+1.8t-0.12t2=10+1.8 · 10-0.12 · 102=16 m/s2

Por tanto, la aceleración inicialmente vale 10 m/s2, crece hasta t=7.5 s, momento en el que adquiere su valor máximo, y luego vuelve a disminuir hasta 16 m/s2. Por tanto, la aceleración mínima en el intervalo es la del instante inicial:

amín=10 m/s2