a) v1=4.56 m/s
b) v2=3.72 m/s
c) vmáx=4.98 m/s; t=1.412 s
d) t= 3.26 s
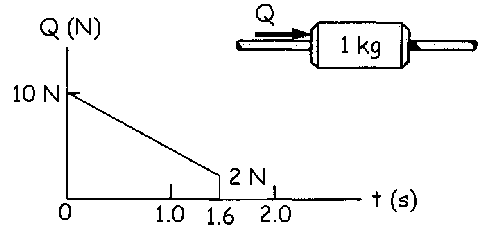
a) La fuerza Q actúa entre t=0 y t=1.6 s. Como dicha fuerza es variable, la aceleración también es variable, luego no se pueden aplicar las ecuaciones del movimiento rectilíneo uniformemente acelerado. Utilizaremos aquí el teorema del impulso. Para ello necesitamos las expresiones de las fuerzas que actúan sobre la deslizadera.
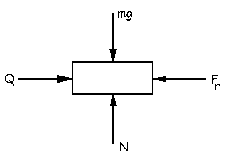 Realizamos el diagrama de sólido libre de la deslizadera. Tomamos como eje X el horizontal hacia la derecha, y como eje Y el vertical hacia arriba. Tendremos por la segunda ley de Newton:
Realizamos el diagrama de sólido libre de la deslizadera. Tomamos como eje X el horizontal hacia la derecha, y como eje Y el vertical hacia arriba. Tendremos por la segunda ley de Newton:
S
Fy=0 Þ
N-mg=0 Þ
N=mg
Como el sistema desliza, la fuerza de rozamiento adquiere su valor máximo:
Fr=(Fr)máx=µN=µmg=0.3 · 1 · 9.8=2.94 N=cte
La fuerza Q sigue la ecuación de una recta luego su expresión será del tipo:
Q=a-bt
Conocemos dos puntos por los que pasa esta recta:
t=0 Þ
Q=10 N Þ
10=a
t=1.6 s Þ
Q=2 N Þ
2=a-bt Þ
2=10-1.6b Þ
b=5
La fuerza Q por tanto tiene la expresión:
Q=a-bt=10-5t
Para t=1 s en el eje X actúan la fuerza Q y la de rozamiento. Aplicando a este eje el teorema del impulso y teniendo en cuenta que la deslizadera parte del reposo:
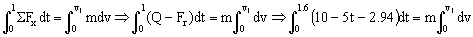
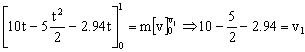
v1=4.56 m/s
b) Ahora tenemos dos intervalos. Desde t=0 hasta t=1.6 s actúa la fuerza F, luego tenemos el mismo caso de antes, pero hasta t=1.6 s:
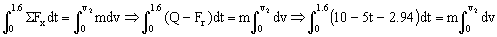
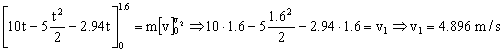
A continuación tenemos una segunda etapa, desde t=1.6 s hasta t=2 s (un tiempo de 0.4 s), en la que Q ya no actúa y sólo tendríamos la fuerza de rozamiento. Como dicha fuerza es constante, el movimiento es rectilíneo uniformemente acelerado. La aceleración podemos determinarla a partir de la segunda ley de Newton:
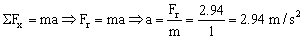
Como el movimiento es uniformemente decelerado:
vF=v0-at Þ
v3=v2-at=4.896-2.94 · 0.4=3.72 m/s
v3=3.72 m/s
c) Si la velocidad es máxima, su derivada respecto del tiempo será nula. En este caso:
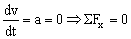
Además, la velocidad debe ser máxima dentro del intervalo en el que actúa Q, ya que después el movimiento es uniformemente decelerado y la deslizadera disminuye su velocidad. Tendremos entonces:
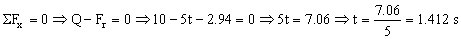
t=1.412 s
Para este tiempo tendremos, que aplicando el teorema del impulso:
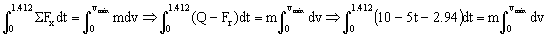
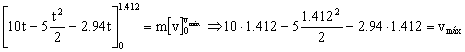
vmáx=4.98 m/s
d) La deslizadera se parará después de t=1.6 s. Después de este instante ya habíamos visto que el movimiento era rectilíneo uniformemente decelerado, y que la aceleración valía 2.94 m/s2. Tendremos entonces:
vF=v0-at Þ
0=4.896-2.94t´ Þ
t´=1.66 s
Este tiempo es el que transcurre desde que la fuerza Q deja de aplicarse hasta que la deslizadera se para, luego habrá que añadirle los 1.6 s durante los cuales la fuerza Q se aplica:
t=1.6+t´=1.6+1.66=3.26 s
t=3.26 s