a) vmáx=9.04 m/s
b) v=0.55 m/s
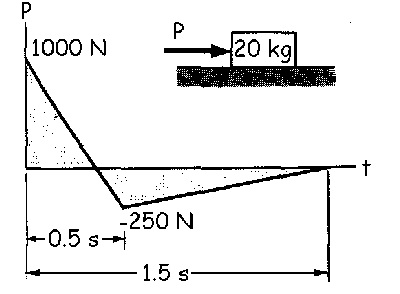
a) Tenemos dos tramos para la fuerza P. En primer lugar, desde t=0 hasta t=0.5 s la expresión de P será la de una recta de pendiente negativa, es decir, del tipo:
P1=a-bt
Conocemos dos puntos por los que pasa esta recta:
t=0 ⇒ P1=1000 N ⇒ 1000=a
t=0.5 s ⇒P1=-250 N ⇒ -250=1000-0.5b ⇒ b=2500
La ecuación de la fuerza P en este intervalo es:
P1=a-bt=1000-2500t
El segundo intervalo va desde t=0.5 s hasta t=1.5 s. En este tramo la ecuación de P será la de una recta de pendiente positiva:
P2=c+dt
Conocemos también dos puntos de esta recta:
t=0.5 s ⇒ P2=-250 N ⇒ -250=c+0.5d
t=1.5 s ⇒ P2=0 ⇒ 0=c+1.5d ⇒ c=-1.5d
Sustituyendo la segunda expresión en la primera:
-250=c+0.5d ⇒ -250=-1.5d+0.5d ⇒ -250=-d ⇒ d=250
Y el parámetro c:
c=-1.5d=-1.5 · 250=-375
Luego en este segundo intervalo la expresión de la fuerza P es:
P2=c+dt=-375+250t
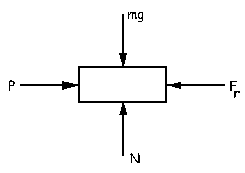Sobre el bloque actúan las fuerzas que aparecen en el gráfico. Tomaremos como ejes el eje X horizontal y hacia la derecha y el eje Y vertical y hacia arriba. Aplicando la segunda ley de Newton:
ΣFy=0 ⇒ N-mg=0 ⇒ N=mg
Como el bloque desliza la fuerza de rozamiento adquiere su valor máximo:
Fr=(Fr)máx=µN=µmg=0.25 · 20 · 9.8=49 N=cte
Existe una fuerza P variable, luego la aceleración también será variable y no podemos aplicar las ecuaciones del movimiento rectilíneo uniformemente acelerado. Usaremos por tanto el teorema del impulso, teniendo en cuenta que el móvil únicamente se mueve en el eje X y que parte del reposo.
La velocidad se tiene que hacer máxima en el primer intervalo, ya que en ese intervalo P pasa de ser positiva a negativa e iría en sentido contrario al movimiento. A partir de ahí P vuelve a crecer pero por debajo del cero. Entonces, la condición de velocidad máxima, que se produciría en el primer intervalo, será que la derivada de la velocidad respecto del tiempo sea nula:
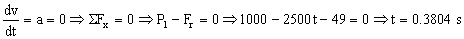
Para este tiempo se producirá la velocidad máxima. Aplicando el teorema del impulso desde el instante inicial hasta ese momento:
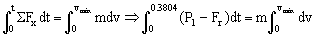
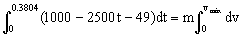
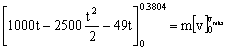
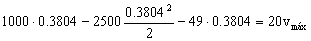
vmáx=9.04 m/s
b) Ahora tendremos que dividir el movimiento en dos tramos, desde t=0 a t=0.5 s y desde t=0.5 s hasta t=1.5 s. Para el primer intervalo:
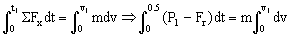
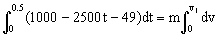
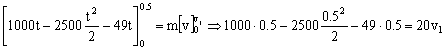
De donde obtenemos la velocidad al final del primer intervalo:
v1=8.15 m/s
Para el segundo intervalo la fuerza P tiene la expresión P2 y tendremos:
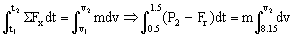
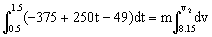
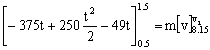
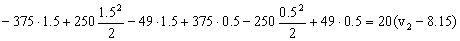
De donde obtenemos la velocidad final:
v2=-0.55 m/s