a) t=2.54 s; h=19.18 m
b) v= ± 4.9 m/s

a) Cuando las bolas se crucen implicará que ambas están a la misma altura, que denominaremos y. La aceleración a que ambas están sometidas es la de la gravedad, g, y el movimiento de las dos es rectilíneo uniformemente acelerado. Las velocidades iniciales de ambas son iguales:

v₀=20 m/s

Y el tiempo que están en el aire lo representaremos por t para la primera bola, y por (t-1) para la segunda bola, que es lanzada 1 s después. Cuando ambas están a la altura y tendremos para la primera bola:

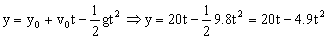
Y para la segunda bola:

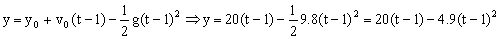
Como las bolas se cruzan a la misma altura podemos igualar estas dos ecuaciones:

20t-4.9t²=20(t-1)-4.9(t-1)² ⇒ 20t-4.9t²=20t-20-4.9t²-4.9+9.8t ⇒ 9.8t-24.9=0

De donde obtenemos el tiempo t que tardan las bolas en cruzarse:

t=2.54 s

Y la altura correspondiente:

y=20t-4.9t²=20 · 2.54-4.9 · 2.54²=19.18 m

y=19.18 m

b) Para la primera bola la velocidad será:

v_F1=v₀-gt=20-9.8 · 2.54=-4.9 m/s

v_F1= -4.9 m/s

Y para la bola segunda:

v_F2=v₀-g(t-1)=20-9.8 · (2.54-1)=4.9 m/s

v_F2= 4.9 m/s

Los signos significan que mientras la bola primera ya está bajando, la segunda aún está subiendo.