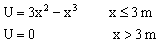a) x=0; x=2 m; x>3 m
b) 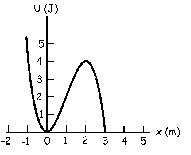
c) x=0 ⇒ equilibrio estable; x= 2 m ⇒ equilibrio inestable; x>3 ⇒ equilibrio indiferente
d) v=2 m/s
a) Si el campo de fuerzas es conservativo la fuerza es el gradiente de la energía potencial cambiado de signo:
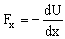
En este caso, para x£
3 m tendríamos que la fuerza vale:
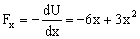
Veamos en qué puntos se anula esta fuerza:
-6x+3x2=0 ⇒ x(-6+3x)=0
Hay una solución inmediata que es:
x=0
Y el otro factor es:
-6+3x=0 ⇒ x=2 m
x=2 m
Para x>3 m tenemos que la energía potencial es constante e igual a cero, luego su derivada también será nula. Esto implica que cuando x>3 m la fuerza siempre es nula:
x>3 m
b) Representemos ahora la energía potencial en función de x. Para x>3 m no tenemos que hacer nada, ya que la energía potencial a partir de ahí es nula. Representaremos sólo para x<3 m, para lo cual hacemos una tabla de datos. Sabemos que la energía potencial en esta zona vale:
U=3x2-x3
Realizamos así la tabla:
|
U (J) |
4.961 |
4 |
2.432 |
1.296 |
0.544 |
0.128 |
0 |
0.416 |
1.408 |
2.592 |
3.584 |
|
x (m) |
-1.1 |
-1 |
-0.8 |
-0.6 |
-0.4 |
-0.2 |
0 |
0.4 |
0.8 |
1.2 |
1.6 |
Tendremos la gráfica que aparece a continuación:
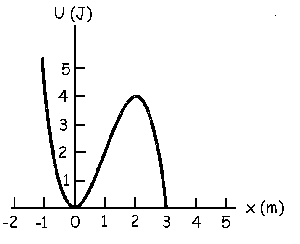
c) Para ver el tipo de equilibrio tendremos que ver si la partícula se encuentra en un máximo o en un mínimo de la curva de energía potencial. Si en ese punto la curva de energía potencial presenta un máximo la partícula estará en equilibrio inestable, mientras que si la curva presenta un mínimo la partícula estará en equilibrio inestable. Para ver si el punto es máximo o mínimo tendremos que ver si la segunda derivada es positiva o negativa. Empezaremos por el intervalo en que x≤3 m. La segunda derivada vale:
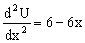
En el punto x=0 tendremos que el valor de la derivada es:
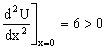
Como la segunda derivada es positiva, la partícula se encuentra en un mínimo y el equilibrio es estable:
x=0 £ EQUILIBRIO ESTABLE
Para x=2 m:
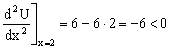
Como la segunda derivada es negativa la partícula se encuentra en un máximo de la curva de potencial y el equilibrio es inestable:
x=2 m ⇒ EQUILIBRIO INESTABLE
Cuando x>3 m la curva de potencial tiene la expresión:
U=0
Es una constante, luego la gráfica sería horizontal y el equilibrio es indiferente:
x>3 m ⇒ EQUILIBRIO INDIFERENTE
d) Cuando x=2 m la energía potencial es (tener en cuenta que estamos en el intervalo en que x<3 m):
U=3x2-x3=3 · 22-23=12-8=4 J
La energía total es suma de la cinética más la potencial, luego conociendo la potencial y la total podemos determinar la cinética:
ET=EC+U ⇒ EC=ET-U=12-4=8 J
Y teniendo en cuenta la expresión de la energía cinética:
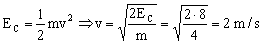
v=2 m/s