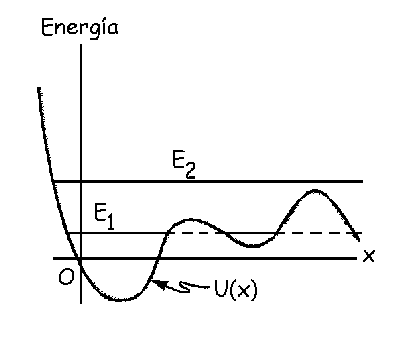
⇒

a) cuando la energía es E₁, está permitido el movimiento para valores de x comprendidos entre los correspondientes a los puntos A y B, entre los C y D y por encima de E; cuando la energía es E2 para valores de x por encima del correspondiente a F
b) para los casos en que su energía corresponda a la de los puntos G,H,I ó J
c) energías y posiciones inferiores a las correspondientes al punto J
d) puntos H y J ⇒ equilibrio inestable; G e I ⇒ equilibrio estable

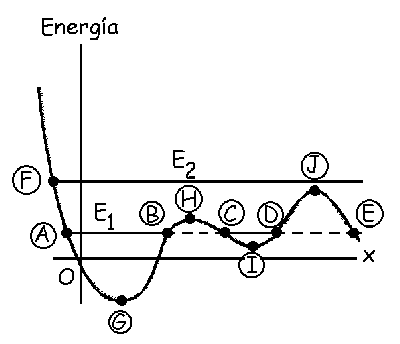
a) Tendremos siempre que la energía total es constante, y además es suma de potencial más cinética. En la gráfica vemos que para cualquier punto, desde el eje X hasta la curva U(x) mediríamos la energía potencial, y desde la curva hasta el nivel de energía total (E₁ ó E₂) mediríamos la cinética:

E_T=E_P+E_C

Para la energía E₁ la partícula debe moverse entre los puntos A y B, entre los puntos C y D o por encima del punto E, porque fuera de estos puntos, por ejemplo, entre B y C, la energía potencial es mayor que la energía total, lo que hace que para que se cumpla la ecuación:

E₁=E_P+E_C

como E₁<E_P la energía cinética debería ser negativa, lo que es imposible, ya que:

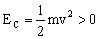
Por tanto la partícula siempre debe restringir su movimiento a zonas de la gráfica en que la curva de potencial esté por debajo de la recta de energía total. Para E₁ estos puntos son entre los puntos A y B, entre los puntos C y D y por encima del punto E.

CUANDO E=E₁ f1feb01 ENTRE A y B, ENTRE C y D, POR ENCIMA DE E

 

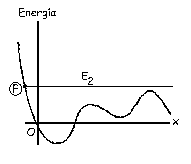Si la energía vale E₂ ocurre exactamente lo mismo. Para que la energía cinética sea positiva la curva de potencial debe estar por debajo de la de energía total. En este caso tendremos que la partícula debe moverse por encima del punto F.

CUANDO E=E₂ f1feb01 POR ENCIMA DE F

 

b) Para que la partícula esté en reposo su energía cinética debe ser nula y debe estar en una posición de equilibrio. Este equilibrio se consigue si la suma de las fuerzas es igual a cero:

ΣF_x=0

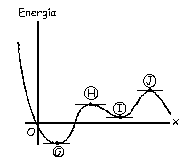Como la fuerza deriva del potencial:

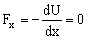
Gráficamente la derivada es la pendiente de la tangente en el punto dado. Si queremos que la pendiente sea nula, la tangente debe ser horizontal. Por tanto la partícula está en equilibrio cuando la tangente a la curva en el punto dado sea horizontal, es decir, en los puntos G, H, I y J; y si la energía de la partícula es la correspondiente a esos puntos está en reposo .

PUNTOS G, H, I y J

 

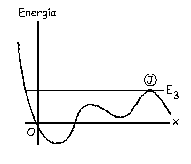c) Para que el movimiento de la partícula esté dentro de puntos de retorno la energía total debe ser tal que esté por encima de la curva de potencial y que además la corte en dos puntos. Por la izquierda no tendríamos problema, ya que independiente de la energía total que tomemos, dicha recta siempre cortará a la curva de potencial por la izquierda. Por la derecha la recta de energía total cortará a la curva de potencial siempre que esté por debajo del máximo más alto, es decir, del punto J. Entonces tendremos que la partícula está dentro de puntos de retorno cuando:

E<E₃

d) Las posiciones de equilibrio de la partícula son aquéllas en las que se cumple que:

F_x=0

Por tanto son las que hemos determinado en el apartado b), y por las mismas razones que explicamos entonces.

EQUILIBRIO: PUNTOS G, H, I, J

 

Veamos ahora qué tipo de equilibrio tienen estos puntos. Empecemos por el punto H. Supongamos que desplazamos la partícula de la posición de equilibrio, por ejemplo, hacia la izquierda, es decir, en sentido negativo. La pendiente de la tangente entonces es positiva, lo que implica que la fuerza, que tiene signo contrario, es negativa, es decir, como el desplazamiento. Aparecería una aceleración en el mismo sentido que haría alejarse a la partícula cada vez más de la posición de equilibrio. Tendríamos entonces que el punto H es un punto de equilibrio inestable, ya que al separar ligeramente a la partícula de la posición de equilibrio, ésta tiene a alejarse cada vez más de dicho punto. Lo mismo ocurre con el punto J, que es análogo al H.

Veamos ahora el punto G. Supongamos que desplazamos la partícula del punto G hacia la izquierda (sentido negativo). La pendiente de la tangente es entonces negativa, y la fuerza, que tiene signo contrario, es positiva. Aparece por tanto una fuerza de sentido contrario al desplazamiento que tiende a hacer regresar a la partícula a su posición de equilibrio. Este punto sería por tanto un punto de equilibrio estable, ya que al alejar a la partícula de su posición de equilibrio ésta tiende a volver a él. Lo mismo ocurriría con el punto I.

PUNTOS H y J: EQUILIBRIO INESTABLE

PUNTOS G e I: EQUILIBRIO ESTABLE