Lo primero que tenemos es que la partícula no puede alcanzar valores negativos de x, luego la curva de energía potencial tiende a infinito cuando x=0 y tiene que estar situada en la parte del eje x de valores positivos.

Si tenemos tres regiones en las que la partícula se mueve dentro de puntos de retorno debemos de tener tres pozos de potencial (tres mínimos).

Como la partícula no puede llegar al infinito, la velocidad debe hacerse cero antes, con lo cual la energía potencial tenderá a infinito para valores finitos de x.. Tendremos entonces una barrera de potencial, de modo que sea cual sea la energía que pongamos, la recta que la representa siempre debe cortar a la curva de potencial por la derecha.

Por último, la partícula tiene posiciones de equilibrio inestable en x=1 nm y x=2 nm. Como son posiciones de equilibrio, en ellas se cumplirá que las fuerzas son nulas:

F_x=0

Como el campo de fuerzas deriva del potencial:

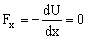
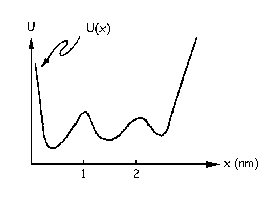Geométricamente la derivada es la pendiente de la tangente en el punto dado. Si esa pendiente debe ser nula, la tangente será horizontal, lo que sólo puede ocurrir si la curva pasa por máximos o por mínimos. Como el equilibrio debe ser inestable, la curva pasará por máximos, de modo que al desplazar la partícula del punto de equilibrio se genera una fuerza del mismo signo que el desplazamiento que tiende a hacer alejar a la partícula de esa posición de equilibrio. La gráfica que cumple todas estas condiciones podría ser la que aparece en la figura.