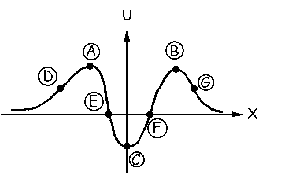
a) puntos A y B: equilibrio inestable; punto C: equilibrio estable
b) puntos D, E, F y G
a) Si el campo de fuerzas deriva del potencial se cumplirá que:
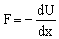
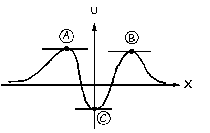
Geométricamente, la derivada de una función es la pendiente de la tangente en el punto dado. Tendremos entonces que los puntos de equilibrio serán aquéllos en los que la fuerza neta es nula: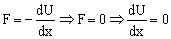 
. Esto implica que la pendiente de la tangente a la curva tiene que ser nula. Esto se cumplirá cuando la tangente sea horizontal, es decir, en los puntos que hemos marcado en la gráfica como A, B y C.
PUNTOS A, B y C
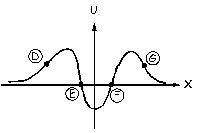
Veamos ahora qué tipo de equilibrio tienen estos puntos. Empecemos por el punto A. Supongamos que desplazamos la partícula de la posición de equilibrio, por ejemplo, hacia la izquierda, es decir, en sentido negativo. La pendiente de la tangente entonces es positiva, lo que implica que la fuerza, que tiene signo contrario, es negativa, es decir, como el desplazamiento. Aparecería una aceleración en el mismo sentido que haría alejarse a la partícula cada vez más de la posición de equilibrio. Tendríamos entonces que el punto A es un punto de equilibrio inestable, ya que al separar ligeramente a la partícula de la posición de equilibrio, ésta tiene a alejarse cada vez más de dicho punto. Lo mismo ocurre con el punto B, que es análogo al A. Veamos ahora el punto C. Supongamos que desplazamos la partícula del punto C hacia la izquierda (sentido negativo). La pendiente de la tangente es entonces negativa, y la fuerza, que tiene signo contrario, es positiva. Aparece por tanto una fuerza de sentido contrario al desplazamiento que tiende a hacer regresar a la partícula a su posición de equilibrio. Este punto sería por tanto un punto de equilibrio estable, ya que al alejar a la partícula de su posición de equilibrio ésta tiende a volver a él.
PUNTOS A y B: EQUILIBRIO INESTABLE. PUNTO C: EQUILIBRIO ESTABLE
b) Dado que la fuerza en módulo vale: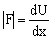 
y la derivada es la pendiente de la tangente, el módulo de la fuerza es máximo cuando la pendiente de la tangente sea máxima. Esto se produce en los puntos de inflexión de la curva, es decir, en los puntos D, E, F y G, siendo los de módulo mayor E y F:
PUNTOS E y F
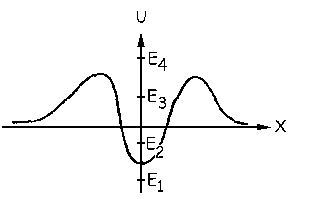
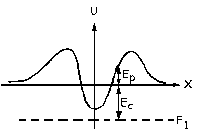c) Vamos a ver el tipo de movimiento de una partícula con energía E1. En la gráfica nos aparece la energía potencial. Por tanto, como la energía total es constante, en todos los puntos se cumplirá que: E1=EC+EP. La distancia desde el cero hasta la gráfica nos dará la energía potencial, y desde la gráfica hasta la recta de E1 nos dará la cinética. Podemos ver que si la partícula tiene una energía E1 en todo momento se cumple que: E1<EP. Lo que implica que como: E1=EC+EP ⇒ EC<0. Esto es imposible, ya que: 
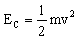, y siempre es un valor positivo. El movimiento de una partícula con energía E1 es por tanto imposible.
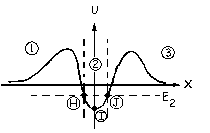Para la energía E2 la gráfica nos quedaría dividida en tres partes, que hemos marcado como 1, 2 y 3. Puede verse que en las zonas 1 y 3 nos ocurre como en el caso anterior, la energía total es menor que la potencial, lo que implicaría que la energía cinética debe ser negativa. Como esto no es posible, la partícula no podría moverse en estas zonas, y estaría confinada a moverse en la zona 2, entre los puntos H y J. En esta zona tendríamos que en el punto H la energía total y la potencial coinciden, luego la energía cinética tiene que ser nula. La partícula en este punto partiría sin velocidad, desde el reposo. Desde el punto H hasta el I la energía potencial disminuye; como la energía total es constante, aumentará la cinética, luego la partícula aumenta su velocidad, es decir, acelera. Desde I hasta J ocurre lo contrario; la energía potencial aumenta luego disminuye la cinética, lo que quiere decir que la partícula está frenando. En el punto J la energía total coincide con la potencial y la cinética sería nula, deteniéndose la partícula. A partir de aquí invertiría el sentido de su movimiento, y empezaría a ir hacia I acelerando y de I a H decelerando y así sucesivamente.
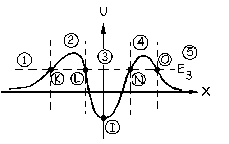Si la energía total es E3, podemos dividir la gráfica en cinco partes (1, 2, 3, 4 y 5). En las zonas 2 y 4 el movimiento no está permitido porque la energía total es inferior a la potencial y ya hemos visto que esto no puede ser. La partícula se podría mover sólo en las zonas 1, 3 y 5, y no puede pasar de una a otra porque eso implicaría tener una energía cinética negativa. En la parte 1 la partícula vendría moviéndose desde el infinito hasta el punto K. En este intervalo la energía potencial aumenta luego la cinética disminuye, es decir, la partícula viene decelerando. En el punto K la energía potencial y la total coinciden luego la cinética es nula y la partícula se detiene momentáneamente. A continuación invertiría su movimiento e iría desde el punto K hasta el infinito acelerando (la energía potencial disminuye). En la parte 3 tenemos lo mismo que hemos visto para la energía E2 pero entre los puntos L y N. En L la partícula parte del reposo y acelera hasta el punto I donde la energía potencial es mínima y por tanto la cinética es máxima (velocidad máxima). Desde I hasta N la partícula decelera deteniéndose en N e invirtiendo su movimiento. En la parte 5 el movimiento es análogo a la parte 1. La partícula parte del reposo en el punto O (la energía total y la potencial coinciden ⇒ la energía cinética, y por tanto la velocidad, es nula) y acelera hasta el infinito (la energía potencial disminuye).
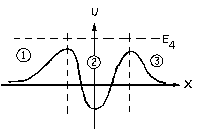Por último, para la energía E4 en ningún punto la curva de energía potencial está por encima de la energía total, luego el movimiento está permitido en todo el intervalo. Podemos hablar de tres zonas empezando por la izquierda. En la zona 1 la energía potencial aumenta luego la cinética disminuye, luego la partícula viene desde el infinito disminuyendo su velocidad. En la zona 2 la energía potencial disminuye hasta un mínimo y luego aumenta, luego la velocidad de la partícula aumenta y después disminuye. Y en la zona 3 la energía potencial disminuye luego la cinética aumenta, y la partícula irá acelerando hasta el infinito. En ningún momento se produce una parada del móvil, ya que en ningún momento la energía total y la potencial coinciden.