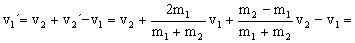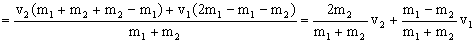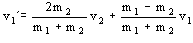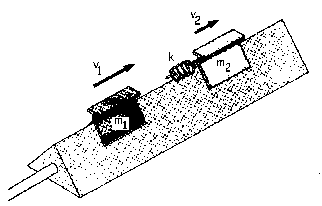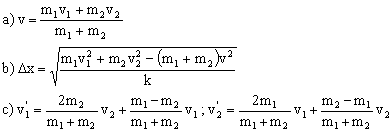
a) Cuando el móvil 1 toca el resorte éste empieza a comprimirse, de modo que el móvil 1 empieza a disminuir su velocidad, mientras que la de m2 aumenta. Cuando el resorte está con su máxima compresión la velocidad de ambos móviles será la misma (la llamaremos v). A partir de ahí el móvil 1 tendría menos velocidad que el móvil 2, empezaría a separarse de él y el resorte se descomprime. Entonces cuando tenemos la máxima compresión la velocidad de los dos móviles es la misma.
Además, como no existen fuerzas externas se conserva la cantidad de movimiento o momento lineal del sistema.:
m1v1+m2v2= m1v+m2v ⇒
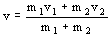
b) Aplicaremos ahora la conservación de la energía entre la posición que llamaremos 1 inmediatamente antes de que los móviles entren en contacto, y la posición 2 cuando el resorte está con su máxima compresión. No tendremos en cuenta la energía potencial gravitatoria, ya que ésta se mantiene constante en todo el proceso:
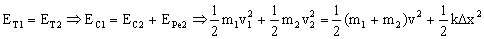
m1v12+m2v22=(m1+m2)v2+kΔx2
De donde:
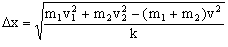
c) Por último, aplicando nuevamente la conservación de la cantidad de movimiento así como la de la energía cinética antes y después del choque. Marcaremos como «primas» a las velocidades de los móviles después del choque. Tendremos entonces:
pantes=pdespués ⇒ 1v1+m2v2=m1v1´+m2v2´
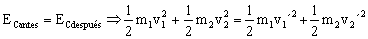
Simplificando y reordenando:
m1(v1-v1´)=m2(v2´-v2)
m1(v12-v1´2)=m2(v2´2-v22)
En la segunda ecuación podemos sustituir la diferencia de cuadrados por el producto de la suma por la diferencia:
m1(v1-v1´)=m2(v2´-v2)
m1(v1-v1´)(v1+v1´)=m2(v2´-v2)(v2´+v2)
Simplificando en la segunda ecuación los términos que la primera ecuación nos dice que son iguales nos queda el sistema:
m1(v1-v1´)=m2(v2´-v2)
v1+v1´=v2´+v2
De la segunda ecuación:
v1´=v2+v2´-v1
Y sustituyendo en la primera:
m1(v1-v1´)=m2(v2´-v2) ⇒ m1(v1-v2-v2´+v1)=m2(v2´-v2) ⇒
m1v1-m1v2+m1v1+m2v2=m1v2´+m2v2´
2m1v1+v2(m2-m1)=v2´(m1+m2)
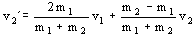
Y la otra velocidad: