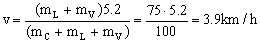a) v=5.2 km/h
b) v=3.9 km/h
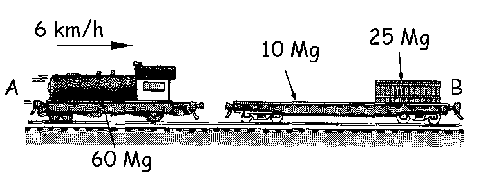
Vamos a considerar por un lado la carga aislada de masa mc y por otro el sistema formado por la locomotora de masa mLy el vagón de masa mv.
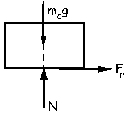 Sobre la carga actúan las fuerzas externas representadas en el diagrama
Sobre la carga actúan las fuerzas externas representadas en el diagrama
N-mcg=0 ⇒ N=mcg
Fr=f N =f mcg (ya que hay deslizamiento)
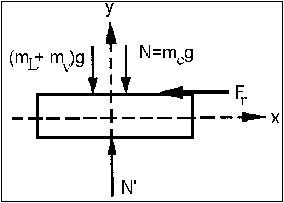 Para el sistema locomotora vagón aislado el diagrama es:
Para el sistema locomotora vagón aislado el diagrama es:
Y respecto a las fuerzas tenemos:
N´-(mL+mv+mc)g=0 ⇒ N=(mL+mv+mc)g
Fr=f mcg
Como el choque sucede instantáneamente el impulso de las fuerzas externas: Frdt podemos considerarlo despreciable ya que el tiempo es infinitamente pequeño y Fr,=fmcg una cantidad finita. Entonces inmediatamente después del choque, la cantidad de movimiento o momento lineal de la carga debe conservarse al igual que debe conservarse la del otro sistema aislado, formado por la locomotora y el vagón.
Para la carga, como inicialmente estaba en reposo inmediatamente después del choque seguirá en reposo, su velocidad es nula
En cuanto al sistema locomotora vagón:
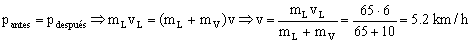
v=5.2 km/h
Siendo de 5.2 km/h la velocidad que tienen la locomotora y el vagón unidos inmediatamente después del choque.
¿Que ha sucedido con la carga que estaba sobre el vagón? Si tenemos:vc=0=vv+vc/v ⇒
vc/v=-vv ⇒ que la carga ha deslizado sobre el vagón con una velocidad igual y de sentido contrario a la del mismo.
b)Después de un cierto tiempo ya no puede despreciarse el valor del impulso, este hace que disminuya la cantidad de movimiento del sistema locomotora vagón y aumente la de la carga hasta que las velocidades de ambos sistemas se igualan y el rozamiento desaparece, a partir de ahí puesto que ya no actúa ninguna fuerza externa la velocidad permanecerá constante. Tenemos:
Frt=mcv-0
-Frt=(mL+mV)v-(mL+mV)5.2
Resolviendo el sistema de ecuaciones:
-mcv =(mL+mV)v-(mL+mV)5.2 ⇒