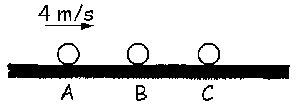vA´=10 m/s; vB´=30 m/s; vB´´=7.5 m/s; vC´=22.5 m/s; vA´´ =8.125 m/s; vB´´´=9.375 m/s
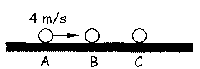 Para el primer choque de A con B podemos plantear dos ecuaciones, la conservación de la cantidad de movimiento y el coeficiente de restitución del choque:
Para el primer choque de A con B podemos plantear dos ecuaciones, la conservación de la cantidad de movimiento y el coeficiente de restitución del choque:
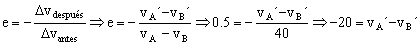
pantes=pdespués ⇒ mvA+mvB=mvA´+mvB´ ⇒ 40=vA´+vB´ ⇒ 40=vA´+vB´
Si sumamos las dos ecuaciones:
20=2vA´
vA´=10 m/s
Y la otra velocidad la sacamos despejando de cualquiera de las dos ecuaciones del sistema:
vB´=vA´+20=10+20=30 m/s
vB´= 30 m/s
 Ahora nos quedan las bolas como aparece en la figura. Como puede verse, B chocará a continuación con C. Podemos plantear las dos mismas ecuaciones, la del coeficiente de restitución y la de conservación del momento lineal. Nos quedará el sistema:
Ahora nos quedan las bolas como aparece en la figura. Como puede verse, B chocará a continuación con C. Podemos plantear las dos mismas ecuaciones, la del coeficiente de restitución y la de conservación del momento lineal. Nos quedará el sistema:
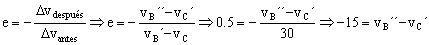
pantes=pdespués ⇒ mvB´+mvC=mvB´´+mvC´ ⇒ 30=vB´´+vC´ ⇒ 30=vB´´+vC´
Sumando las dos ecuaciones obtenidas:
15=2vB´´
vB´´=7.5 m/s
Y la velocidad de C después del choque, a partir de cualquiera de las ecuaciones del sistema:
vC´=vB´´+15=7.5+15=22.5 m/s
vC´=22.5 m/s
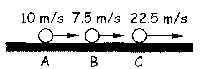 Nos quedan ahora las bolas como indica la figura. Lo siguiente que ocurrirá a la vista de las velocidades es que A vuelva a chocar contra B. Aplicando como antes la conservación del momento lineal y el coeficiente de restitución:
Nos quedan ahora las bolas como indica la figura. Lo siguiente que ocurrirá a la vista de las velocidades es que A vuelva a chocar contra B. Aplicando como antes la conservación del momento lineal y el coeficiente de restitución:
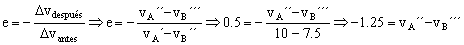
pantes=pdespués ⇒ mvA´+mvB´´=mvA´´+mvB´´´ ⇒ 10+7.5=vA´´+vB´´´ ⇒ 17.5=vA´´+vB´´´
Sumando las ecuaciones:
16.25=2vA´´
vA´´=8.125 m/s
Y la velocidad de B después de este choque:
vB´´´=vA´´+1.25=8.125+1.25=9.375 m/s
vB´´´= 9.375 m/s
 Nos quedan las bolas como se muestra en el gráfico. Como podemos ver, tal como nos han quedado las velocidades no podría producirse ningún otro choque.
Nos quedan las bolas como se muestra en el gráfico. Como podemos ver, tal como nos han quedado las velocidades no podría producirse ningún otro choque.