a) e=0.943
b) h2=0.711m; d=0.377 m
a) El coeficiente de restitución valdrá:
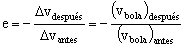
No hemos tenido en cuenta el suelo, que es el otro sistema que participa en el choque, porque es fijo y su velocidad tanto antes como después del choque es nula. Las fuerzas que intervienen en el choque son verticales, luego para el coeficiente de restitución sólo tendremos en cuenta las componentes verticales de la velocidad.
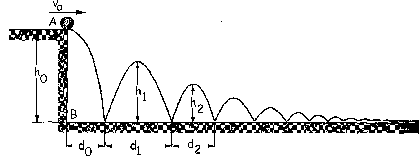
Antes del primer rebote tenemos que la bola cae desde una altura de 0.900 m con velocidad inicial nula en el eje Y. Tendremos movimiento rectilíneo uniformemente acelerado, con aceleración la de la gravedad:
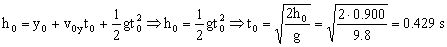
Por tanto, la componente Y de la velocidad inmediatamente antes del primer rebote:
v0=v0y+gt0=gt0=9.8 · 0.429=4.2 m/s
Ya tenemos entonces la velocidad de la bola antes del choque. Después del primer rebote la altura en vez de ser 0.900 m es de 0.800 m, pero haciendo exactamente lo mismo de antes:
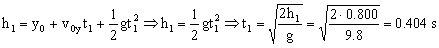
Y ahora tendremos que después del choque la bola parte con una velocidad (en dirección vertical) v1 y llega hasta una altura de 0.800 m (punto en el que la componente vertical de la velocidad se anula) en 0.404 s. Aplicando las ecuaciones del movimiento rectilíneo uniformemente acelerado:
vf=v1-gt1 ⇒ 0=v1-9.8 · 0.404 ⇒ v1=3.960 m/s
Ya tenemos las velocidades de la bola antes y después del primer rebote, luego el coeficiente de restitución es:
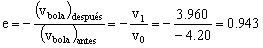
e=0.943
Al sustituir las velocidades hemos tenido en cuenta que v1 es positiva porque es vertical y hacia arriba, y v2 es negativa porque es vertical y hacia abajo.
b) Antes del segundo rebote la velocidad es:
v1=-3.960 m/s
Es igual que la velocidad después del primer rebote pero de signo contrario, ya que son puntos que se encuentran a la misma altura. La velocidad de la bola después del segundo rebote (v2) la podemos determinar a partir del coeficiente de restitución:
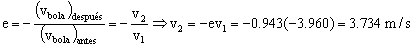
Tendremos entonces que la bola después del segundo rebote parte con una velocidad inicial v2=3.734 m/s y llega al punto de altura h2 (en el cual la componente Y de la velocidad vuelve a ser nula) en un tiempo t2. Aplicando las ecuaciones del movimiento rectilíneo uniformemente acelerado:
vf=v0-gt2 ⇒ 0=3.734-9.8t2 ⇒ t2=0.381 s
Y entonces tendremos que la bola cae desde una altura h2 partiendo del reposo, y llega al suelo en un tiempo t2:
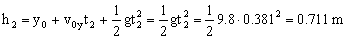
h2=0.711 m
Pasamos ahora a tratar el eje horizontal, que llamaremos eje X. En este eje el movimiento es uniforme. Antes del segundo rebote la bola recorre un espacio d1 en un tiempo 2t1 (el doble del que tarda en alcanzar la altura máxima) luego para el movimiento rectilíneo uniforme:
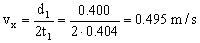
Esta velocidad es constante, luego después del segundo rebote el tiempo que tarda la bola en recorrer el espacio d2 será 2t2 luego:
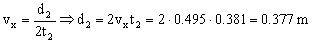
d2=0.377 m