a) P=20833N
b) F_railes=31177 N
c) θ=131.9^o

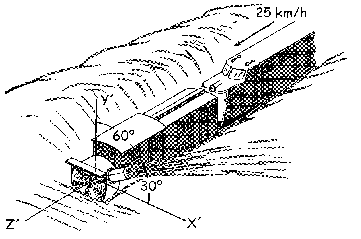
a) La velocidad del quitanieves es la misma que la de la locomotora, puesto que van unidos:

v_Q=25 km/h=6.94 m/s

Vectorialmente, tal como tenemos los ejes de la figura:

v_Q=6.94k

La velocidad de la nieve respecto del quitanieves es:

v_N/Q=12cos30ºi+12sen30ºj=10.39i+6j

Si queremos la velocidad absoluta de la nieve tendremos:

v_N/Q=v_N–v_Q Þ v_N=v_N/Q+v_Q=10.39i+6j+6.94k

Podemos aplicar el teorema del impulso al quitanieves, y nos quedará:

ΣFdt=dp_N ⇒ F_QNdt=dmv_N ⇒

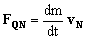
La variación de masa por unidad de tiempo es:

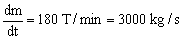
Por tanto:

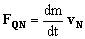Þ F_QN=3000(10.39i+6j+6.94k)=31177i+18000j+20833k

La componente en Z de esta fuerza debe compensarse con la reacción de la locomotora, para que la locomotora se mueva con velocidad constante, luego:

P=-20833k N

En módulo:

P=20833 N

b) Para que la locomotora no se mueva lateralmente, la componente X de la fuerza F_QN debe compensarse con la ejercida por los raíles:

F_raíles=-31177i N

Y en módulo:

F_raíles=31177 N

 

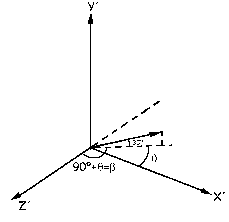c) Ahora tenemos el sistema que muestra la figura para la velocidad relativa. La velocidad relativa de la nieve respecto del quitanieves es ahora:

v_N/Q=12cos30ºcosθi+12sen30ºj-12cos30ºsenθk=12.39cosθi+6j-10.39senθk

 

La velocidad de la nieve entonces será:

v_N/Q=v_N–v_Q

v_N=v_N/Q+v_Q=10.39cosθi+6j-10.39senθk+6.94k

Por tanto la fuerza ejercida por el quitanieves es:

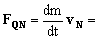
=3000(10.39cosθi+6j-10.39senθk+6.94k)=31170cosθi+18000j-31170senθk+20820k

La reacción sobre el eje Z debe ser cero:

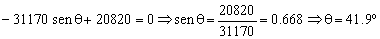
El ángulo pedido es:

β=90º+θ=90º+41.9º=131.9º

θ=131.9º