a) Fr=26444 N
b) v=829.5 km/h
a) La velocidad del avión es:
vA=800 km/h=222.2 m/s
Vamos a aplicar el teorema del impulso, que dice que:
ΣFdt=dp
Tomaremos como eje X el de avance del avión, y como eje Y el perpendicular a él. Llamaremos va a la velocidad del aire. Para determinarla tenemos en cuenta la velocidad relativa:
va/A=va–vA ⇒ va=va/A+vA=-600i+222.2i=-377.78i m/s
Vamos a hacer un esquema con tres gráficos. En el primero de ellos representaremos el primer miembro, es decir, todas las fuerzas aplicadas sobre el sistema. A continuación representaremos el segundo miembro como la diferencia de cantidad de movimiento entre dos instantes muy próximos, en t, y en t+dt. Inicialmente tendremos el avión moviéndose a velocidad vA que toma aire en reposo. Un instante después, el avión expulsaría una cantidad de aire dm a velocidad va por la parte posterior del avión. Así, tendremos el diagrama:
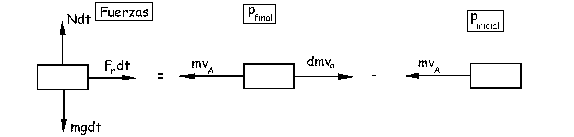
Para el eje X:
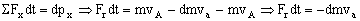
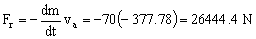
Fr=26444.4 N
b) Ahora tenemos que la fuerza de resistencia es proporcional al cuadrado de la velocidad del avión, es decir:
Fr=KvA2
siendo K la constante de proporcionalidad. Sabemos que cuando la velocidad del avión es de 222.2 m/s la fuerza de rozamiento vale 26444.4 N, luego podemos determinar con estas condiciones la constante:
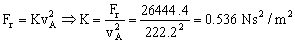
Y la fuerza de rozamiento:
Fr=KvA2=0.536vA2
El flujo de aire además ha aumentado un 10% luego ahora vale:
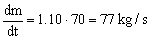
La velocidad absoluta del aire ha variado, luego tendremos:
va/A=va–vA ⇒ va=va/A+vA=-va/Ai+vAi=(vA-va/A)i
Aplicando la misma ecuación de antes:
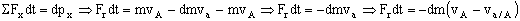
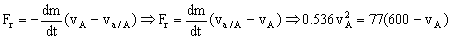
0.536vA2=46200-77vA ⇒ 0.536vA2+77vA-46200=0
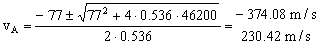
Debemos descartar la solución negativa puesto que hemos definido como positiva la dirección de avance del avión. La solución válida es:
vA=230.42 m/s=829.5 km/h
vA=829.5 km/h