P=mv(gt+v)
Llamaremos M a la masa total de la cadena. Si m es la masa por unidad de longitud y l la longitud total de la cadena:
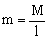
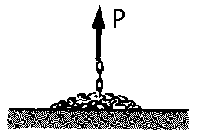 El sistema al cual se incorpora masa es el tramo vertical de la cadena. La masa que se incorpora está en reposo sobre el suelo. Denominaremos m0 a la masa de cadena vertical, cuya longitud será y variable. Entonces:
El sistema al cual se incorpora masa es el tramo vertical de la cadena. La masa que se incorpora está en reposo sobre el suelo. Denominaremos m0 a la masa de cadena vertical, cuya longitud será y variable. Entonces:
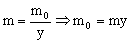
Utilizaremos ecuaciones escalares, ya que todo el movimiento se realiza en el eje vertical. Tomaremos como sentido positivo el vertical hacia arriba. Aplicando el teorema del impulso lineal:
ΣFdt=dp
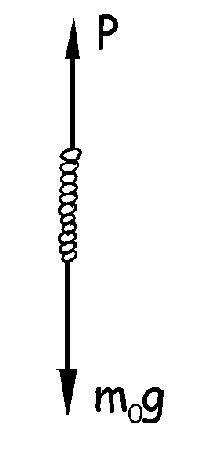 Aislamos el tramo vertical de la cadena. Tendremos en cuenta que en un tiempo t se incorpora masa a la cadena pero con velocidad nula, luego no aportaría cantidad de movimiento, y en un tiempo t+dt tendríamos una cantidad de masa dm0 que se movería hacia arriba a velocidad v. Nos queda la ecuación:
Aislamos el tramo vertical de la cadena. Tendremos en cuenta que en un tiempo t se incorpora masa a la cadena pero con velocidad nula, luego no aportaría cantidad de movimiento, y en un tiempo t+dt tendríamos una cantidad de masa dm0 que se movería hacia arriba a velocidad v. Nos queda la ecuación:
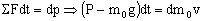
Dividimos a los dos miembros por dt:
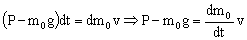
Y ahora tenemos en cuenta que:
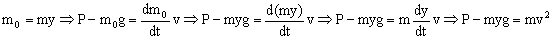
Como la velocidad v es constante:
y=vt
Luego sustituyendo:
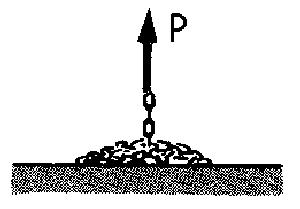
P-myg=mv2 v P-mgvt=mv2 ⇒ P=mgvt+mv2=mv(gt+v)
P=mv(gt+v)