a) a_t=75 m/s²
b) a_t=300 m/s²

a) El cohete con el combustible es un sistema de masa variable, ya que la masa va disminuyendo a medida que se utiliza el combustible. Tomaremos como eje X el del movimiento del cohete, y como positivo su sentido de avance. En este caso, si es v la velocidad del cohete en cada instante, v_g la velocidad del combustible, y v_g/c la velocidad del combustible respecto del cohete:

v_g/c=v_g–v ⇒ v_g=v_g/c+v=(-2500+v)i

 

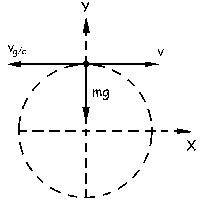Aplicaremos el teorema del impuso al eje X:

ΣF_xdt=dp_x

 

En el eje X no se aplicaría ninguna fuerza sobre el cohete (ver diagrama donde aparecen tanto fuerzas como velocidades); en cuanto a la variación de la cantidad de movimiento tendremos que en un instante t el cohete avanza a velocidad v, mientras que un instante t+dt, la masa del cohete será m-dm avanzando a una velocidad v+dv, y además saldría una cantidad de gases dm a velocidad v_g; entonces:

(ΣF_x)_extdt=dp_x ⇒ 0=(m-dm)(v+dv)+dm(v-v_g/c)-mv ⇒ 0=mv+mdv-dmv-dmdv+dmv-v_g/cdm-mv

El término dmdv podemos despreciarlo por ser un infinitésimo de segundo orden, y nos quedará:

0=mdv-2500dm

Si dividimos a todo por dt:

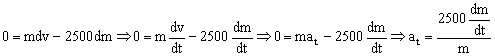
En el momento en que se encienden los motores la masa del cohete es de 500 kg luego la aceleración tangencial:

a_t=75 m/s²

b) En el momento en que se ha consumido la última partícula de combustible la masa será únicamente la del cohete:

m=500-375=125 kg

Luego la aceleración tangencial:

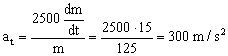
a_t=300 m/s²