C_x=0; C_y= 1600 N; D=2400 N

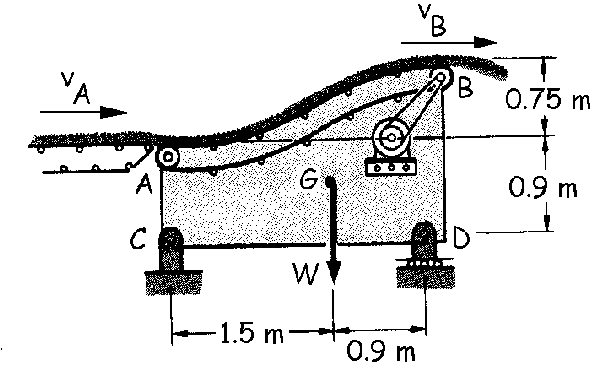
Tomaremos como eje X el horizontal hacia la derecha, y como eje Y el vertical hacia arriba. D es un apoyo de rodillo que sólo proporcionará reacción normal. Vamos a aplicar el teorema del impulso.

Para ello trazaremos unos diagramas. En uno de ellos representaremos las fuerzas aplicadas sobre el sistema. En los otros expresaremos la variación del momento lineal. Tendremos que en un instante t entra en el sistema una cantidad de masa dm a velocidad v_A, mientras que un instante después, en t+dt sale del sistema la misma masa dm a la misma velocidad, que el problema llama v_B. Tendremos el diagrama que aparece en la figura. Si aplicamos el teorema del impulso lineal al eje X:

ΣF_xdt=dp_x ⇒ C_xdt=dmv_B-dmv_A

Como v_B=v_A=4 m/s

C_x=0

Para el eje Y haciendo exactamente lo mismo:

ΣF_ydt=dp_y ⇒ (C_y-mg+D)dt=dmv_B-dmv_A

Por lo mismo de antes:

(C_y-mg+D)dt=0 ⇒ C_y-mg+D=0 ⇒ C_y-4000+D=0

Tenemos una ecuación con dos incógnitas. Ahora podemos aplicar el teorema del impulso angular:

Dividimos los dos miembros por dt:

2.4D-6000=80[-v_B(0.75+0.9)+v_A · 0.9 ] ⇒ 2.4D-6000=-80 · 4 · 1.65+80 · 4 · 0.9

D=2400 N

Y la reacción C_y:

C_y-4000+D=0 ⇒ C_y=4000-D=4000-2400=1600 N

C_y=1600 N