a) T=2s; ν=0.5 s^-1
b) x=senπt
c) v=cosπt; a=-senπt
d) x=0.5 m; v=2.72 m/s; a=-4.93 m/s²
e) v_máx=π m/s

a) Para el período tendremos:

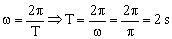
T=2 s

Y para la frecuencia, teniendo en cuenta que es el inverso del período:

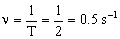
ν=0.5 s^-1

 

b) La ecuación del movimiento será del tipo:

x=Asen(ωt+φ₀)

siendo ω la frecuencia angular y φ₀ el ángulo de fase inicial.

Sabemos que cuando t=0 ⇒ x=0, luego sustituyendo estas condiciones en la ecuación:

x=Asen(ωt+φ₀) ⇒ 0=Asenφ₀ ⇒ senφ₀=0 ⇒ φ₀=0

Por tanto la ecuación del movimiento es:

x=Asen(ωt+φ₀)=1senπt=senπt

x=senπt

 

c) La velocidad es:

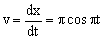
v=πcosπt

Y la aceleración:

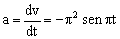
a=-π²senπt

 

d) Para 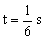tendremos que la elongación vale:

x=0.5 m

La velocidad:

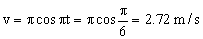
v=2.72 m/s

Y la aceleración:

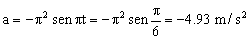
a=-4.93 m/s²

e) Si la elongación vale -0.5 m tendremos:

 

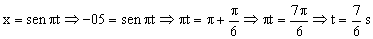
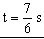
f) La velocidad vale:

v=πcosπt

El único término variable es el del coseno, luego la velocidad será máxima cuando el coseno sea máximo, es decir, cuando valga la unidad:

cosπt=1 ⇒ v_máx=π m/s

v_máx=π m/s