a) t=1.55 s
b) vmáx=-0.808 m/s
c) amáx=-3.26 m/s2
d) v=-0.70 m/s; a=-1.635 m/s2
e) t=0.259 s
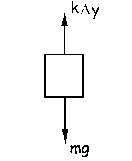 a) En primer lugar el problema nos dice que colgamos del resorte un peso de 500 g y el resorte se alarga 15 cm. Si hacemos el diagrama de sólido libre del resorte en esta situación de equilibrio, y tomamos como eje Y el vertical tendremos:
a) En primer lugar el problema nos dice que colgamos del resorte un peso de 500 g y el resorte se alarga 15 cm. Si hacemos el diagrama de sólido libre del resorte en esta situación de equilibrio, y tomamos como eje Y el vertical tendremos:
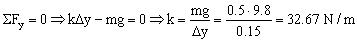
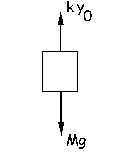 Ahora suspendemos del resorte un cuerpo de 2 kg. Para la posición de equilibrio de este nuevo cuerpo tendremos que el resorte se alarga una cantidad y0:
Ahora suspendemos del resorte un cuerpo de 2 kg. Para la posición de equilibrio de este nuevo cuerpo tendremos que el resorte se alarga una cantidad y0:
ΣFy=0 ⇒ ky0-Mg=0
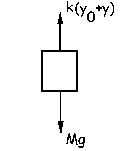 Ahora desplazamos el sistema hacia abajo una cantidad y y lo dejamos oscilar. En ese caso:
Ahora desplazamos el sistema hacia abajo una cantidad y y lo dejamos oscilar. En ese caso:
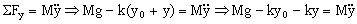
Teniendo en cuenta la condición de equilibrio podemos eliminar los términos Mg-ky0 por ser nulos y nos queda:
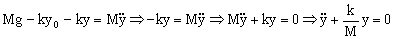
Es la ecuación de un m. a. s. del tipo:
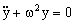
De donde deducimos por comparación:
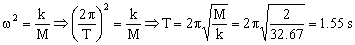
T=1.55 s
b) Como es un movimiento armónico simple, la ecuación de la elongación será:
y=Asen(ωt+φ0)
donde A es la amplitud, ω la frecuencia angular y φ 0 el ángulo de fase inicial. La amplitud, que sería la máxima elongación, nos dice el enunciado que es de 20 cm:
A=20 cm=0.2 m
La frecuencia angular es:
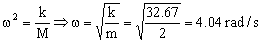
Además, como condiciones iniciales tenemos que para t=0 ⇒ y=A luego:
y=Asen(ωt+φ0) ⇒ A=Asenφ0 ⇒ senφ0=1 ⇒ φ0=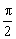
Por tanto la ecuación que nos da la posición en función del tiempo es:
y=Asen(ωt+φ0)=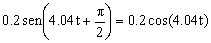
La velocidad será la derivada del espacio respecto del tiempo:
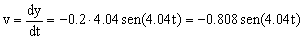
En esa ecuación el único término variable es el seno, luego la velocidad será máxima cuando el seno tome su valor máximo, es decir, la unidad:
sen(4.04t)=1 ⇒ vmáx=-0.808 m/s
vmáx=-0.808 m/s
c) La aceleración es la derivada de la velocidad respecto del tiempo:
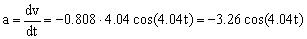
En esta ecuación el único término variable es el coseno, luego la aceleración será máxima cuando el coseno tome su valor máximo, que es la unidad:
cos(4.04t)=1 ⇒ amáx=-3.26 m/s2
amáx=-3.26 m/s2
d) Si el móvil se encuentra a mitad de camino entre la posición de equilibrio y una de sus posiciones extremas la elongación valdrá:
y=0.1 m ⇒ 0.1=0.2cos(4.04t) ⇒ cos(4.04t)=0.5 ⇒ 4.04t=1.047 ⇒ t=0.259 s
Entonces la velocidad vale:
v=-0.808sen(4.04t)=-0.808sen(4.04 · 0.259)=-0.7 m/s
v=-0.7 m/s
Y la aceleración:
a=-3.26cos(4.04t)=-3.26cos(4.04 · 0.259)=-1.635 m/s2
a=-1.635 m/s2
e) El tiempo necesario para alcanzar el citado punto ya lo hemos determinado:
t=0.259 s