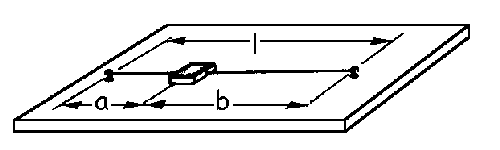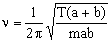
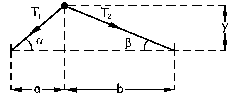
Si la oscilación es pequeña, al desplazar el bloque podemos seguir suponiendo que la tensión casi no varía y que sigue siendo T. Trazamos el diagrama de sólido libre y denominamos y a la dirección en que realizamos el desplazamiento. En el eje X, que sería el perpendicular, no habría movimiento y tendríamos:

ΣF_x=0 ⇒ T₁cosα-T₂cosβ=0

Si las oscilaciones son muy pequeñas los ángulos α y β también lo serán, por lo que podemos realizar la aproximación:

cosα » 1; cosβ » 1

De donde obtenemos:

T₁cosα-T₂cosβ=0 ⇒ T₁-T₂=0 ⇒ T₁=T₂=T

Ahora para el eje Y tenemos:

Como hemos dicho que estos ángulos son muy pequeños, sus senos pueden aproximarse a las respectivas tangentes:

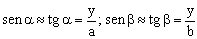
Sustituyendo esto en la expresión que teníamos:

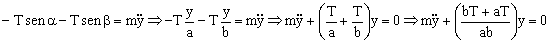
Como vemos hemos llegado a la ecuación de un movimiento armónico simple cuya frecuencia angular es:

 

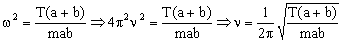
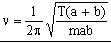
La frecuencia será mínima cuando sea máximo el denominador de esa ecuación que es:

D=mab=ma(l-a)=mal-ma²

 La condición de máximo es que la derivada sea igual a cero luego:

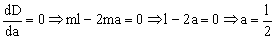
Y teniendo en cuenta que a+b=l:

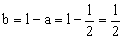
Por tanto:

 

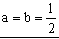
Demostraremos además, que la condición obtenida es un máximo para el denominador D y no un mínimo, en cuyo caso habríamos hecho lo mismo. Para que sea un máximo debe cumplirse además que la segunda derivada sea negativa. Si volvemos a derivar:

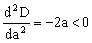
Luego efectivamente, para ese valor la frecuencia presenta un mínimo.
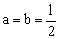