a) v_A=120 mm/s hacia arriba
b) v_D=120 mm/s hacia abajo

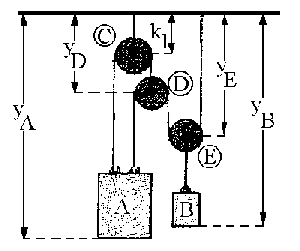
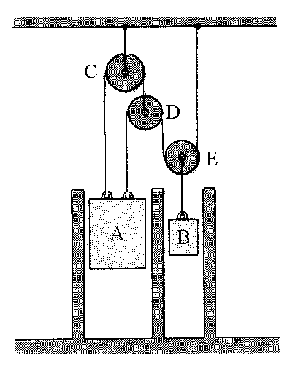
a) Tendremos lo que se muestra en la figura. Llamaremos y_A, y_B, y_D e y_E a las posiciones en cada instante de los bloques A y B y de las poleas D y E respectivamente. Como las poleas y los bloques únicamente se mueven en el eje Y, las derivadas de estos parámetros respecto del tiempo serán las respectivas velocidades, es decir:

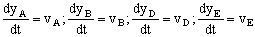
Llamaremos k₁ y k₂ a las longitudes de las barras que unen la polea C con el techo y la polea E con el bloque B. Además, nombraremos como r_C, r_D y r_E a los radios de las poleas C, D y E. Con esto, tendremos que la longitud de la cuerda que une el bloque A con la polea D es:

l₁=y_A-k₁+π
r_C+y_D-k₁=y_A+y_D-2k₁+πr_C

Esta longitud se mantiene constante en el tiempo, luego su derivada respecto del tiempo será cero. Si derivamos esa expresión teniendo en cuenta que las derivadas de los términos constantes son nulas obtenemos:

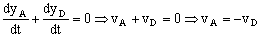
La longitud de la cuerda que une el bloque A con el techo valdrá:

l₂=y_A-y_D+πr_D+y_E-y_D+πr_E+y_E= y_A-2y_D+πr_D+πr_E+2y_E

Igual que antes, como esta longitud es constante, su derivada respecto del tiempo es nula, luego si derivamos esa expresión, teniendo en cuenta que las derivadas de todas las constantes son cero tendremos:

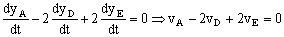
Como antes hemos obtenido que v_A es igual a -v_D:

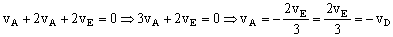
Además, podemos ver en el dibujo que:

y_E=y_B+k₂

Derivando respecto del tiempo:

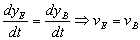
Y nos dan como dato la velocidad del bloque B luego tendremos:

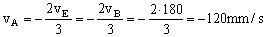
v_A=-120 mm/s

b) Y la velocidad del bloque D:

v_D=-v_A=120 mm/s

v_D=120 mm/s