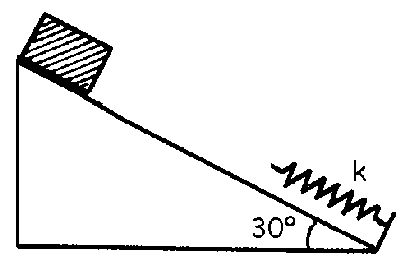
Problema de Movimiento Oscilatorio

Un resorte ideal sin masa se puede comprimir 1 m mediante una fuerza de 100 N. Este mismo resorte se coloca en la parte inferior de un plano inclinado 30o con respecto a la horizontal. Una masa m de 10 kg se suelta desde la parte superior del plano partiendo del reposo, y queda en reposo momentáneo después de comprimir el resorte 2 m. Determinar: a) ¿qué distancia resbala la masa antes de quedar en reposo? b) ¿cuál es la velocidad de la masa cuando está a punto de hacer contacto con el resorte?

a) l=4.08 m
b) v=4.52 m/s

a) En primer lugar determinaremos la constante del resorte, teniendo en cuenta que bajo una fuerza de 100 N el resorte se comprime 1 m:

Ahora vamos a aplicar la conservación de la energía mecánica entre las posiciones que denominaremos 1, cuando el bloque se suelta desde el reposo en la parte de arriba del plano inclinado, y 2, después de que el resorte se comprime 2 m. Suponemos que el rozamiento entre la masa y el plano inclinado es nulo.

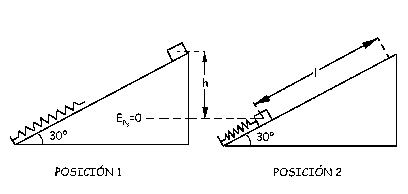
ET1=ET2 ⇒ EPg1=EPe2

l=4.08 m

 

b) Ahora aplicamos la conservación de la energía total entre la misma posición que antes hemos llamado 1 y la posición que llamaremos 3, en la cual el bloque justo toca el resorte.

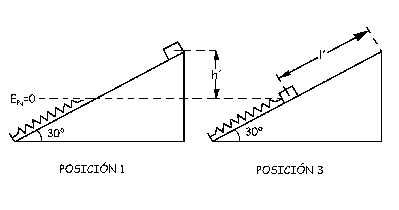
Tendremos que la distancia l´ será la de antes menos los 2 m que estaba comprimido el resorte, es decir:

l´=l-2=4.08-2=2.08 m

Tendremos entonces:

v=4.52 m/s