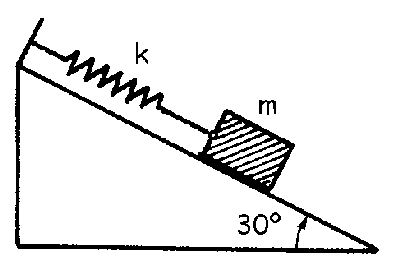
a) l=0.299 m
b) ν=1.59 s-1
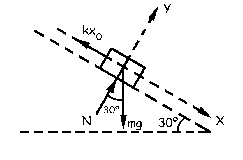a) Para la posición de equilibrio tendremos lo que aparece en la figura. Aplicando la segunda ley de Newton:
ΣFx=0 ⇒ mgsen30º-kx0=0
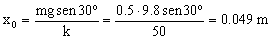
La longitud del resorte en esa posición será la longitud natural del resorte más su elongación:
l=l0+x0=0.25+0.049=0.299 m
l=0.299 m
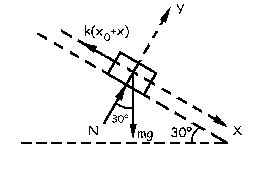b) A continuación desplazamos el bloque hacia abajo y lo dejamos oscilar. Tendremos entonces:
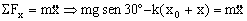
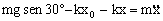
Tenemos de la condición de equilibrio que: mgsen30º-kx0=0
Con lo cual nos queda:
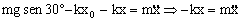
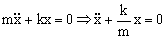
Es la ecuación de un movimiento armónico simple de frecuencia angular:
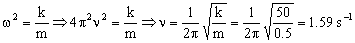
ν=1.59 s-1