a) T=2.84 s
b) v=1.98 m/s; Ec=0.392 J; F=2.352 N
c) 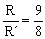
d) T´=2.42 s
a) Tendríamos un péndulo simple cuyo período será:
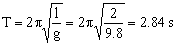
T=2.84 s
b) Como de todas las fuerzas que actúan sobre la esfera la única que realiza trabajo es el peso y es conservativa, la energía total es constante, luego toda la energía potencial que tiene la esfera en el punto de máxima altura debe transformarse en energía cinética al pasar por la vertical:
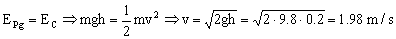
v=1.98 m/s
La energía cinética en ese momento valdrá:
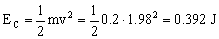
EC=0.392 J
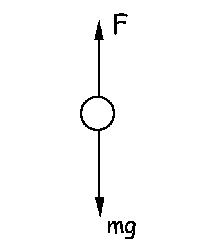 Cuando el péndulo pase por la vertical, estará sometido a las fuerzas que aparecen en la figura. Vertical y hacia abajo tenemos el peso de la esfera, y vertical y hacia arriba la tensión del hilo. En cuanto a aceleraciones, en esa posición la esfera sólo tiene aceleración normal, pues la tangencial at=0 por ser v máxima, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura, es decir, en la misma dirección y sentido que la tensión. Aplicando la segunda ley de Newton:
Cuando el péndulo pase por la vertical, estará sometido a las fuerzas que aparecen en la figura. Vertical y hacia abajo tenemos el peso de la esfera, y vertical y hacia arriba la tensión del hilo. En cuanto a aceleraciones, en esa posición la esfera sólo tiene aceleración normal, pues la tangencial at=0 por ser v máxima, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura, es decir, en la misma dirección y sentido que la tensión. Aplicando la segunda ley de Newton:
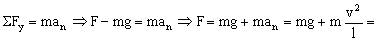
F=2.352 N
c) Al no existir pérdida de energía cinética, la bolita se elevará en el lado de la izquierda una altura vertical de 20 cm, igual a la que se elevaba antes de colocar el clavo. El radio del arco descrito será ahora de 1 m.
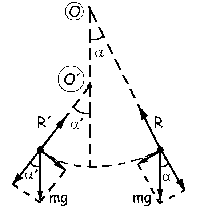 Vamos a ver ahora las tensiones en las posiciones extremas. Llamaremos R a la tensión en el extremo donde el radio del arco descrito es de 2 m (donde no hay clavo) y R´ a la tensión en el extremo en el que el radio del arco descrito es de 1 m (donde sí hay clavo). En el gráfico vemos los diagramas de fuerzas en las dos posiciones extremas. En ambos lados la velocidad es nula, luego la aceleración normal también lo será. Eso significa que en la dirección de la cuerda no hay aceleración, luego la suma de fuerzas en esa dirección es nula. En cada uno de los casos la tensión debe ser igual a la componente del peso en esa dirección:
Vamos a ver ahora las tensiones en las posiciones extremas. Llamaremos R a la tensión en el extremo donde el radio del arco descrito es de 2 m (donde no hay clavo) y R´ a la tensión en el extremo en el que el radio del arco descrito es de 1 m (donde sí hay clavo). En el gráfico vemos los diagramas de fuerzas en las dos posiciones extremas. En ambos lados la velocidad es nula, luego la aceleración normal también lo será. Eso significa que en la dirección de la cuerda no hay aceleración, luego la suma de fuerzas en esa dirección es nula. En cada uno de los casos la tensión debe ser igual a la componente del peso en esa dirección:
R=mgcosα
R´=mgcosα´
Los cosenos de los ángulos podemos determinarlos teniendo en cuenta que en los dos casos la altura sobre el nivel más bajo es de 20 cm:
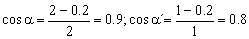
Dividiendo entonces las expresiones de R y R´:
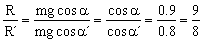
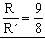
d) El período de este péndulo será el tiempo que tarda la esfera en realizar el recorrido completo ida y vuelta, es decir, en recorrer dos veces α y dos veces α´. El tiempo que tarda en recorrer dos veces el ángulo α será la mitad del período de un péndulo de longitud 2 m, es decir:
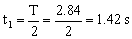
El tiempo que tarda la esfera en recorrer dos veces el ángulo α ´ será la mitad del período de un péndulo de longitud 1 m, es decir:
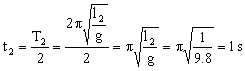
El período del péndulo dado es entonces:
T´=t1+t2=1.42+1=2.42 s
T´=2.42 s