A=6.94; φ=38.58o
Tenemos dos movimientos armónicos simples en la misma dirección. El movimiento resultante será la suma de ambos:
x=x1+x2
Y además será del tipo:
x=Asen(ωt+φ)
donde A es la amplitud y φ la constante de fase. Sustituyendo cada movimiento por su expresión tenemos:
x=x1+x2 ⇒ Asen(ωt+φ)=3sen(ωt+30º)+4sen(ωt+45º)
Desarrollamos el seno de una suma teniendo en cuenta que vale:
sen(a+b)=senacosb+cosasenb
Nos quedará:
Asenωtcosφ+Acosωtsenφ=3senωtcos30º+3cosωtsen30º+4senωtcos45º+4cosωtsen45º
Igualamos por separado los términos que llevan el factor cosωt (proyecciones sobre el eje horizontal) y los términos que llevan el factor senωt (proyecciones sobre el eje vertical):
Asenωtcosφ=3senωtcos30º+4senωtcos45º
Acosωtsenφ=3cosωtsen30º+4cosωtsen45º
Simplificando y poniendo los valores conocidos:
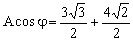
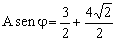
Dividiendo la segunda expresión entre la primera:
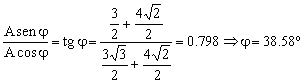
φ=38.58º
Y la amplitud a partir de una cualquiera de las ecuaciones en que aparece:
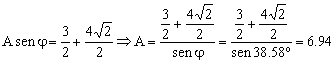
A=6.94