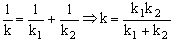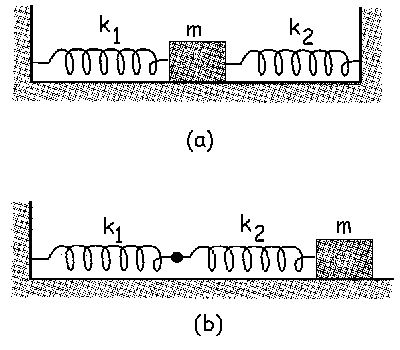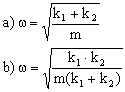
Para todo el ejercicio y para los dos casos consideraremos unos ejes cartesianos normales, con el eje X horizontal y el eje Y vertical.
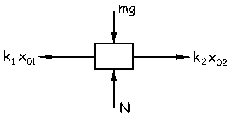 a) En la posición de equilibrio, si realizamos el diagrama del sólido libre del cuerpo tendremos lo que se muestra en la figura. Denominaremos x01 y x02 a las elongaciones de los dos resortes en la posición de equilibrio. Como el sistema está en reposo:
a) En la posición de equilibrio, si realizamos el diagrama del sólido libre del cuerpo tendremos lo que se muestra en la figura. Denominaremos x01 y x02 a las elongaciones de los dos resortes en la posición de equilibrio. Como el sistema está en reposo:
ΣFx=0 ⇒ k2x02-k1x01=0
 A continuación desplazamos el bloque una cantidad x hacia la derecha y lo dejamos oscilar. Ahora tendremos:
A continuación desplazamos el bloque una cantidad x hacia la derecha y lo dejamos oscilar. Ahora tendremos:
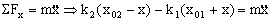
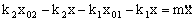
Teniendo en cuenta la condición de equilibrio:
k2x02-k1x01=0
Nos queda:
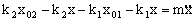
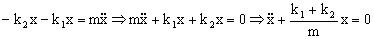
Tenemos la ecuación de un movimiento armónico simple de frecuencia angular:
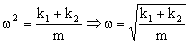
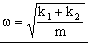
Esta situación sería equivalente aun único resorte de constante k=k1+k2
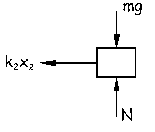 b) Ahora tendremos que en la posición de equilibrio los resortes están sin deformar. Al desplazar el bloque una cantidad x hacia la derecha y dejarlo oscilar, el resorte 1 se alarga una cantidad x1 y el resorte 2 se alarga una cantidad x2.
b) Ahora tendremos que en la posición de equilibrio los resortes están sin deformar. Al desplazar el bloque una cantidad x hacia la derecha y dejarlo oscilar, el resorte 1 se alarga una cantidad x1 y el resorte 2 se alarga una cantidad x2.
Para el bloque tendremos:
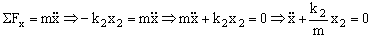
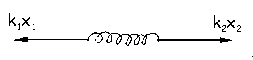 Para tener la ecuación de un movimiento armónico simple necesitamos relacionar x con x2. Para ello aislamos el resorte 2, con lo que tendremos que como dicho resorte tiene masa despreciable:
Para tener la ecuación de un movimiento armónico simple necesitamos relacionar x con x2. Para ello aislamos el resorte 2, con lo que tendremos que como dicho resorte tiene masa despreciable:
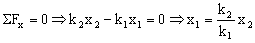
El desplazamiento x vale:
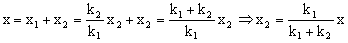
Sustituyendo en la ecuación que teníamos para el bloque:
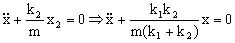
Es la ecuación de un movimiento armónico simple de frecuencia:
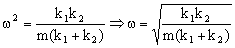
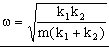
Situación equivalente a un único resorte de constante k tal que: