x1=0.0715 m; x2=0.0456 m; T1=10.725 N; T2=7.296 N
En primer lugar pasamos la velocidad angular a rad/s:
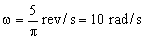
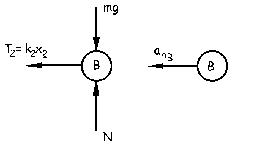 Llamaremos eje X al eje en el que está situado el tubo con los resortes y las bolitas. Si aislamos la bolita B, dibujando tanto las fuerzas como las aceleraciones a las que está sometida tendremos:
Llamaremos eje X al eje en el que está situado el tubo con los resortes y las bolitas. Si aislamos la bolita B, dibujando tanto las fuerzas como las aceleraciones a las que está sometida tendremos:
ΣFx=max ⇒ T2=manB ⇒ k2x2=mω2rB
donde x2 es la elongación del resorte R2 y rB es el radio de curvatura de la trayectoria seguida por la bolita B. Si llamamos l1 y l2 a las longitudes naturales de los resortes 1 y 2, y x1 y x2 a las elongaciones de los mismos en el equilibrio dinámico tendremos que el radio de curvatura de la trayectoria seguida por la bolita B es:
rB=l1+l2+x1+x2=0.5+0.6+x1+x2=1.1+x1+x2
Sustituyendo en la ecuación de fuerzas de la bolita B:
k2x2=mω2rB ⇒ 160x2=0.06·102(1.1+x1+x2) ⇒ 160x2=6.6+6x1+6x2 ⇒ 154x2-6x1=6.6
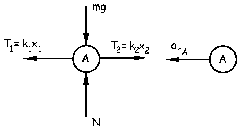 Ahora realizamos el diagrama de sólido libre de la bolita A en esas mismas condiciones. Tendremos:
Ahora realizamos el diagrama de sólido libre de la bolita A en esas mismas condiciones. Tendremos:
ΣFx=max ⇒ T1-T2=manA ⇒ k1x1-k2x2=mω2rA
Sustituimos como antes los datos conocidos, teniendo en cuenta que el radio de curvatura de la trayectoria seguida por la bolita A es:
rA=l1+x1=0.5+x1
k1x1-k2x2=mω2rA ⇒ 150x1-160x2=0.06 · 102(0.5+x1) ⇒ 150x1-160x2=3+6x1 ⇒ 144x1-160x2=3
Tenemos dos ecuaciones y dos incógnitas:
154x2-6x1=6.6
144x1-160x2=3
Multiplicamos a la primera ecuación por 24:
3696x2-144x1=158.4
144x1-160x2=3
Y ahora sumamos las dos ecuaciones:
3536x2=161.4 ⇒ x2=0.0456 m
x2=0.0456 m
Y ahora de una cualquiera de las ecuaciones despejamos x1:
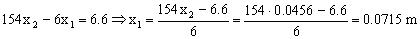
x1=0.0715 m
Y las tensiones en los dos resortes son:
T1=k1x1=150·0.0715=10.725 N
T1=10.725 N
T2=k2x2=160·0.0456=7.296 N
T2=7.296 N
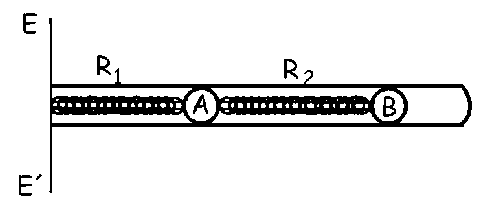
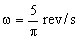 . Las bolitas A y B de igual masa m=60 g resbalan sin rozamiento a lo largo del tubo. Si las longitudes de los resortes R1 y R2, sin deformar, son 50 cm y 60 cm, y sus constantes elásticas 150 N/m y 160 N/m respectivamente, calcule el aumento de longitud de cada resorte y las tensiones en cada uno de ellos.
. Las bolitas A y B de igual masa m=60 g resbalan sin rozamiento a lo largo del tubo. Si las longitudes de los resortes R1 y R2, sin deformar, son 50 cm y 60 cm, y sus constantes elásticas 150 N/m y 160 N/m respectivamente, calcule el aumento de longitud de cada resorte y las tensiones en cada uno de ellos.