a) T=0.294 s; ν=3.403 s^-1
b) v_máx=0.428 m/s; a_máx=9.142 m/s²

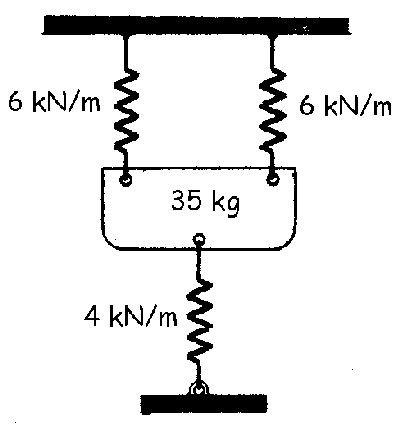
a) Denominaremos eje Y al eje en que se produce el movimiento, es decir, al eje vertical. A los dos resortes de la parte superior le marcaremos con el subíndice 1 (el mismo para ambos puesto que son iguales) y al resorte de la parte inferior le marcaremos con el subíndice 2.

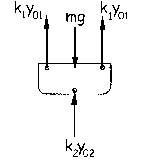
En primer lugar vamos a determinar lo que ocurre cuando el bloque está en equilibrio. Si está en equilibrio tendremos lo que aparece en la figura. Aplicando la segunda ley de Newton (se ha supuesto que el muelle 1 está a tracción y el 2 a compresión):

ΣF_y=0 ⇒ mg-2k₁y₀₁-k₂y₀₂=0

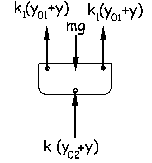A continuación desplazamos el bloque hacia abajo una cantidad y y lo dejamos oscilar. Tendremos entonces:

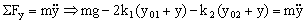
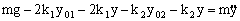
Sabemos por la condición de equilibrio que:

mg-2k₁y₀₁-k₂y₀₂=0

Por tanto eliminando estos términos de la ecuación diferencial:

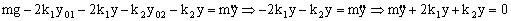
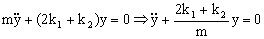
Tenemos la ecuación de un movimiento armónico simple de frecuencia angular:

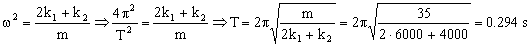
T=0.294 s

Y la frecuencia es el inverso del período:

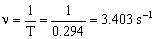
ν=3.403 s^-1

 

b) Como el movimiento es armónico simple la ecuación de la posición en función del tiempo será del tipo:

y=Asen(ωt+φ₀)

siendo A la amplitud del movimiento, ω la frecuencia angular y φ₀ la fase inicial. La velocidad entonces será la derivada del espacio respecto del tiempo:

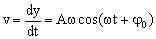
Como la amplitud y la frecuencia angular son constantes, la velocidad será máxima cuando el coseno del ángulo adquiera su valor máximo, es decir, la unidad. Entonces:

v=v_máx ⇒ cos(ωt+φ₀)=1 ⇒ v_máx=Aω

La amplitud del movimiento nos dicen que es de 20 mm y la frecuencia angular vale:

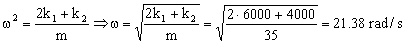
Entonces la velocidad máxima es:

v_máx=Aω=0.02·21.38=0.428 m/s

v_máx=0.428 m/s

Ahora la aceleración será la derivada de la velocidad respecto del tiempo:

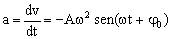
Igual que antes, como la frecuencia angular y la amplitud son constantes la aceleración será máxima cuando lo sea el seno, es decir, cuando valga la unidad:

a=a_máx ⇒ sen(ωt+φ₀)=1 ⇒ a_máx=-Aω²=-0.02·21.38²=-9.142 m/s²

En módulo:

a_máx=9.142 m/s²