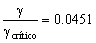
.
La ecuación del movimiento subamortiguado es:
x=A0e-βtsen(ωt+φ0)
donde A0 es la amplitud inicial, β es el parámetro de amortiguamiento, ω la frecuencia angular y φ0 la fase inicial. Podemos considerar entonces que la ecuación es del tipo:
x=A(t)sen(ωt+φ0)
donde la amplitud no es constante, sino que depende del tiempo en la forma:
A(t)=A0e-βt
Para las amplitudes séptima y decimonovena tendremos:
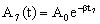
Si dividimos las dos expresiones:
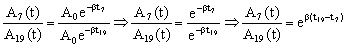
Entre las amplitudes séptima y decimonovena transcurren 12 períodos luego:
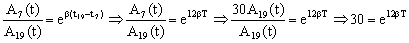
Tomando logaritmos neperianos:
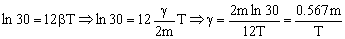
como se trata de un movimiento subamortiguado,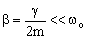 
, y la frecuencia angular del oscilador es,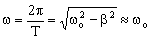 
Si el amortiguamiento es crítico:
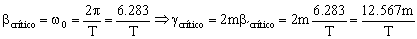
El cociente entonces será:
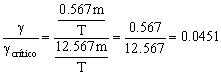
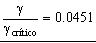
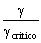