a) y_máxima=7.35 cm
b) sí en 4.58 cm
c) y_máx=5.07 cm

a) La frecuencia natural del oscilador es: 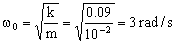. Como β=ω₀ tenemos amortiguamiento crítico. La solución de la ecuación diferencial es:

y=(A₀+A₁t)e^-βt.

Tenemos como condiciones iniciales que cuando t=0 ⇒ y=0 luego: y=(A₀+A₁t)e^-βt ⇒ 0=A₀

Nos queda la ecuación

 y=(A₀+A₁t)e^-βt=A₁te^-βt

Determinaremos ahora la velocidad derivando respecto del tiempo la ecuación de la posición:

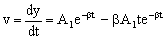
Para t=0 ⇒ v=60 cm/s. Aplicando esta condición:

v=A₁e^-βt-βA₁te^-βt ⇒ 60=A₁ ⇒ A₁=60 cm

Ya tenemos todas las constantes, luego la ecuación de la elongación es:

y=A₁te^-βt=60te^-3t

Y la de la velocidad:

v=A₁e^-βt-βA₁te^-βt=60e^-3t-3·60te^-3t=60e^-3t-180te^-3t

Ahora cuando el desplazamiento es máximo la velocidad es nula luego:

v=0 ⇒ 0=60e^-3t-180te^-3t ⇒ 0=60-180t ⇒ t=0.333 s

Y en ese instante la elongación (que es la máxima) será:

y_máx=60te^-3t=60·0.333e^{-3 · 0.333}=7.35 cm

b) Ahora, aunque el movimiento es el mismo, las condiciones iniciales varían. Vamos a calcular la ecuación, que como antes, será:

y=(A₀+A₁t)e^-βt

Ahora tenemos que para t=0 ⇒ x=4 cm:

y=(A₀+A₁t)e^-βt ⇒ 4=A₀ ⇒ A₀=4 cm

Y la ecuación nos queda:

y=(A₀+A₁t)e^-βt=(4+A₁t)e^-βt

Además tenemos que para t=0 ⇒ v=-60 cm/s; la velocidad es: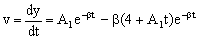

Aplicando las condiciones de contorno:

v=A₁e^-βt-β(4+A₁t)e^-βt ⇒ -60=A₁-4β ⇒ A₁=-48 cm

La ecuación de la posición es:

y=(4+A₁t)e^-βt=(4-48t)e^-3t

Y la velocidad:

v=A₁e^-βt-β(4+A₁t)e^-βt=-48e^-3t-3(4-48t)e^-3t

Para ver si se rebasa la posición de equilibrio vamos a ver cuándo se para el sistema, es decir, cuándo la velocidad es nula:

v=0 ⇒ 0=-48e^-3t-3(4-48t)e^-3t ⇒ 0=-48-3(4-48t) ⇒ 0=-48-12+144t ⇒ 144t=60

t=0.417 s

Para este tiempo la posición es: y=(4-48t)e^-3t=(4-48·0.417)e^{-3 · 0.417}=-4.58 cm

La posición de equilibrio es y=0 luego se rebasa esta posición en 0.58 cm

c) Ahora tenemos como antes que la frecuencia natural de la oscilación es: ω₀=3 rad/s

Como β>ω₀ el movimiento es sobreamortiguado. La solución de la ecuación será:

Las frecuencias son:

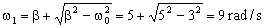
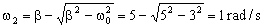
Nos queda la ecuación: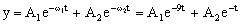

Tenemos que hallar las constantes A₁ y A₂. Como condiciones iniciales tenemos que cuando t=0 ⇒ y=0:

y=A₁e^-9t+A₂e^-t ⇒ 0=A₁+A₂ ⇒ A₁=-A₂

Y además conocemos también las condiciones iniciales de la velocidad. Para determinar la velocidad derivamos respecto del tiempo la ecuación de la posición:

Cuando t=0 ⇒ v=60 cm/s luego: v=-9A₁e^-9t-A₂e^-t ⇒ 60=-9A₁-A₂

Tenemos dos ecuaciones y dos incógnitas:

A₁=-A₂

60=-9A₁-A₂

Sustituyendo en la segunda ecuación lo que hemos obtenido en la primera:

60=-9A₁-A₂ ⇒ 60=9A₂-A₂ ⇒ 60=8A₂ ⇒ A₂=7.5 cm

Y la otra constante: A₁=-A₂=-7.5 cm

Por tanto nos queda una ecuación para la elongación:

y=A₁e^-9t+A₂e^-t=-7.5e^-9t+7.5e^-t

Y para la velocidad:

v=-9A₁e^-9t-A₂e^-t=-9 · (-7.5)e^-9t-7.5e^-t=67.5e^-9t-7.5e^-t

Ahora en el punto de máxima elongación la velocidad es cero:

v=67.5e^-9t-7.5e^-t ⇒ 0=67.5e^-9t-7.5e^-t ⇒ 9e^-9t-e^-t=0 ⇒ 9e^-9t=e^-t

Tomando neperianos:

ln(9e^-9t)=ln(e^-t) ⇒ ln9-9t=-t ⇒ ln9=8t

t=0.275 s

Y con este tiempo la posición (que será la máxima) es:

y_máx=-7.5e^-9t+7.5e^-t=-7.5e^{-9 · 0.275}+7.5e^-0.275=5.07 cm