Problema de Dinámica de la Partícula

El bloque B (mB=10 kg) descansa sobre la plataforma extensa A (mA=20 kg) que a su vez se apoya en el suelo. El coeficiente de rozamiento entre la plataforma y el suelo es 0.1 y entre el bloque y la plataforma 0.5 (no se hace distinción entre los coeficientes de rozamiento estático y cinético). Si se aplica a la plataforma una fuerza horizontal PA; determinar el valor que ha de tener dicha fuerza para que exista movimiento de A y B y para que exista deslizamiento entre A y B.

29.4 < PA < 176.4

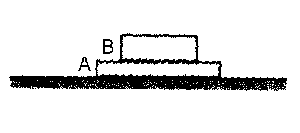
Supongamos en primer lugar que B no desliza sobre A. Como:

aB=aA+aB/A ⇒ aB=aA=a

ya que no existe movimiento relativo de B sobre A. Los dos bloques se mueven como un solo bloque.

Si hacemos el diagrama del sólido libre tendremos:

Aplicando la segunda ley de Newton:

ΣFX=(mA+mB)ax ⇒ PA-Fr´=(mA+mB)a ⇒ PA=Fr´+(mA+mB)a

ΣFY=(mA+mB)aY ⇒ N-(mA+mB)g=0 ⇒ N=(mA+mB)g=(20+10) × 9.8=294 N

La fuerza de rozamiento máxima será:

(Fr´)máx=0.1N=0.1 × 294=29.4 N

Para que los bloques empiecen a moverse, PA ha de superar la fuerza de rozamiento máxima existente entre A y el suelo, luego para que haya movimiento:

PA>29.4 N

Para valores de PA ≤ 29.4 N la aceleración de los cuerpos es nula y como estaban inicialmente en reposo seguirán sin moverse.

PA<29.4 N ⇒ No hay movimiento

Al ir aumentando PA por encima de 29.4 N, empezará a tener un valor la aceleración, que irá aumentando a medida que lo hace PA. Sin embargo, la aceleración de B está limitada por el valor de la fuerza de rozamiento máxima existente entre B y A. Si realizamos el diagrama del sólido libre de los dos bloques por separado tendremos:

Para el bloque B:

ΣFY=mBaY ⇒ NB-mBg=0 ⇒ NB=mBg=10 ×9.8=98 N

ΣFX=mBaX ⇒ Fr=mBaB

La máxima aceleración que puede tener el bloque B se corresponderá con el valor máximo de la fuerza de rozamiento:

(Fr)máx=0.5NB=0.5 × 98=49 N

Fr=mBaB ⇒ 49=10aB ⇒ aB=4.9 m/s2

Si aA>4.9 m/s2, como aB/A=aB-aA existirá deslizamiento entre A y B.

Para la plataforma A tendremos:

ΣFX=mAaX ⇒ PA-Fr-Fr´=mAaA

 

Si aA=aB=4.9 m/s2 entonces:

PA=Fr+Fr´+mAaA=49+29.4+20× 4.9=176.4 N

Luego para valores de PA inferiores o iguales a 29.4 N no existe movimiento, para valores superiores a 29.4 N y hasta 176.4 N se mueven como un bloque, y para valores de PA superiores a 176.4 N existirá deslizamiento entre A y B.

29.4 N<PA<176.4 N ⇒ Movimiento conjunto

PA>176.4 N ⇒ Deslizamiento entre A y B

La aceleración de A irá aumentando a medida que lo hace PA mientras que aB permanecerá constante y será de 4.9 m/s2.