f’ < f

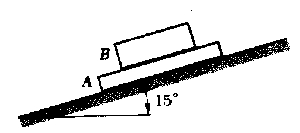
Para que los dos se muevan conjuntamente la fuerza de rozamiento existente entre ambos bloques ha de ser suficiente para evitar el deslizamiento. En el diagrama del sólido libre de ambos bloques y aplicando la segunda ley de Newton tenemos:

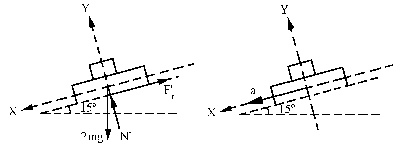
ΣF_Y=2ma_Y ⇒ N´-2mgcos15^o=0 ⇒ N´=2mgcos15^o

ΣF_X=2ma_X ⇒ 2mgsen15^o-F_r´=2ma

Si los bloques deslizan respecto del suelo y llamamos f´ al coeficiente de rozamiento entre el bloque A y el suelo tendremos que:

F_r´=(F_r´)_máx=f´N´=f´2mgcos15^o

Por tanto:

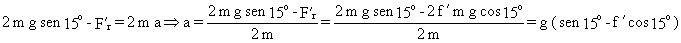
Si ahora aislamos el bloque B y hacemos el diagrama del sólido libre y llamamos f al coeficiente de rozamiento existente entre los dos bloques:

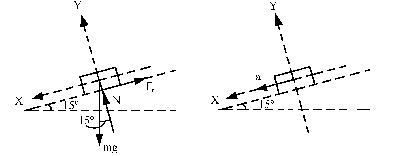
ΣF_Y=ma_Y´⇒ N-mgcos15^o=0 ⇒ N=mgcos15^o

ΣF_X=ma_X´⇒ mgsen15^o-F_r=ma ⇒ F_r=mgsen15^o-ma=

mgsen15^o-mg(sen15^o-f´cos15^o)=f´mgcos15^o

(F_r)_máx=fN=fmgcos15^o

Para que no exista deslizamiento entre los bloques debe cumplirse que:

F_r<(F_r)_máx ⇒ f´mgcos15^o<fmgcos15^o ⇒ f´

f´<f