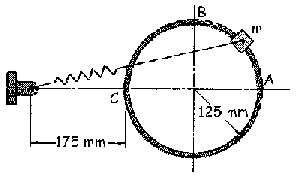
a) vC=2.45 m/s
b) RB=104.92 N;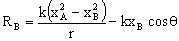 
. No depende de la masa
c) a=92.98 m/s2
d) a=114.86 m/s2, RB=134.32 N
a) Aplicamos la conservación de la energía mecánica entre las posiciones A y B, ya que no hay ninguna fuerza no conservativa que realice trabajo. No tendremos en cuenta la energía potencial gravitatoria ya que como el sistema está en posición horizontal esta energía es constante y es la misma en cualquier punto. Tendremos entonces que en el punto B sólo habrá energía potencial elástica, ya que la cinética es nula puesto que la partícula parte del reposo, mientras que en el punto C sólo tendremos energía cinética, ya que en ese punto el resorte tiene su longitud natural:
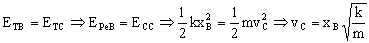
siendo xB la elongación del resorte en el punto B, que valdrá:
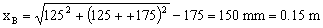
Sustituyendo:
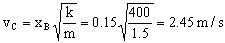
vC=2.45 m/s
b)
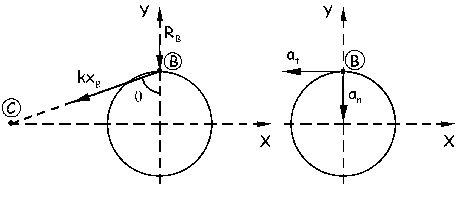
Aislamos la deslizadera en el punto B y trazamos su diagrama de sólido libre. El ángulo θ vale:
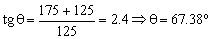
Aplicando la segunda ley de Newton:
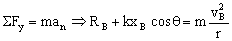
De donde despejamos la reacción en B:
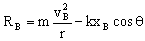
Nos falta calcular la velocidad de la deslizadera en el punto B. Para ello aplicamos la conservación de la energía entre las posiciones A y B. En B tenemos energía potencial elástica y energía cinética, mientras que en A sólo tenemos energía potencial elástica, ya que se suelta la deslizadera desde el reposo en el punto A. Tendremos entonces:
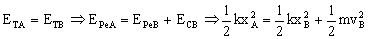
siendo xA la elongación del resorte en el punto A, que vale:
xA=175+125+125-175=250 mm=0.25 m
Sustituyendo:
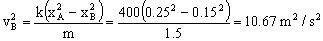
Y la reacción en B:
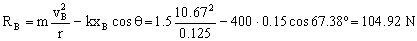
RB=104.92 N
Ahora tenemos que demostrar además que esta reacción no depende de la masa de la deslizadera. Para ello vamos a sustituir en la ecuación que nos da la reacción RB la velocidad en el punto B por su expresión y nos queda:
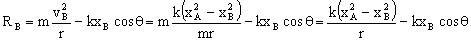
donde podemos ver que efectivamente en la expresión de RB no aparece la masa de la deslizadera.
c) La aceleración tiene dos componentes, la tangencial y la norma. La aceleración normal es sencilla de calcular y vale:
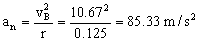
Y para la aceleración tangencial aplicamos de nuevo la segunda ley de Newton al diagrama de sólido libre que habíamos dibujado:
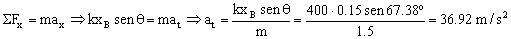
Y teniendo en cuenta que estas dos aceleraciones son perpendiculares, su composición nos da una aceleración total:
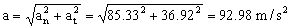
a=92.98 m/s2
d)
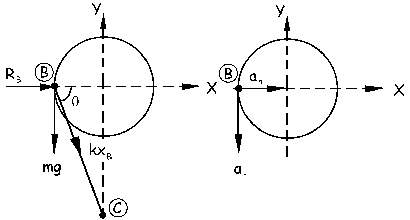
Ahora tenemos el sistema en posición vertical, luego ya influye el peso y además varía la energía potencial gravitatoria dependiendo del punto en que nos encontremos. Para calcular la aceleración y la reacción de la barra en el punto B tendremos que hacer el diagrama de sólido libre en esa situación, y tendremos lo que aparece en la figura. Como puede verse la aceleración tiene dos componentes, la normal y la tangencial. La normal vale:
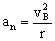
por lo que tendremos que determinar en primer lugar la velocidad de la deslizadera al pasar por el punto B. Para ello aplicamos la conservación de la energía entre las posiciones A, cuando se suelta la deslizadera desde el reposo, y B. En el punto A no tendremos energía potencial gravitatoria, ya que la partícula se suelta desde el reposo, pero tendremos energía potencial gravitatoria y energía potencial elástica, mientras que en B tendremos los tres tipos de energía:
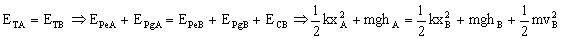
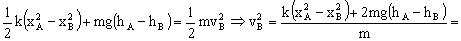
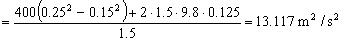
Podemos calcular entonces ya la aceleración normal:
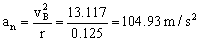
Para la aceleración tangencial aplicamos la segunda ley de Newton al diagrama de sólido libre que tenemos en el gráfico:
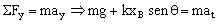
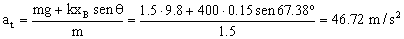
Y la aceleración total será:
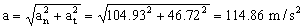
a=114.86 m/s2
Para la reacción en B aplicamos la segunda ley de Newton al eje X del diagrama de sólido libre:
ΣFx=max ⇒ RB+kxBcosθ=man ⇒ RB=man-kxBcosθ=1.5·104.93-400· 0.15cos67.38º=134.32 N
RB=134.32 N