Problema de Gravitación

Aparece en la convocatoria JUN1997

Un satélite de comunicaciones S de 200 kg de masa sigue una órbita circular en torno a la Tierra, en sentido antihorario y a una altura de 200 km sobre la superficie de la misma. Determinar: a) su velocidad; b) el tiempo que tarda en recorrer dicha órbita completa; c) la energía mínima para mantenerlo en órbita; d) para reparar una avería en una de sus antenas se envía desde tierra un vehículo espacial que una vez que ha alcanzado una altura de 100 km y apaga sus motores tiene una velocidad vA=7882.9 m/s en una dirección tal que forma con la vertical un ángulo φ, siguiendo desde ese instante una trayectoria elíptica de aproximación, que llega a ser tangente en B (punto de encuentro) a la trayectoria del satélite. Determinar dicho ángulo φ; e) determinar también el ángulo θ que define la posición del punto A en la órbita elíptica.

a) vS=7804.69 m/s
b) T=5289.19 s
c) ET=-6.09·109 J
d) φ=89.44o
e) θ=65.23o

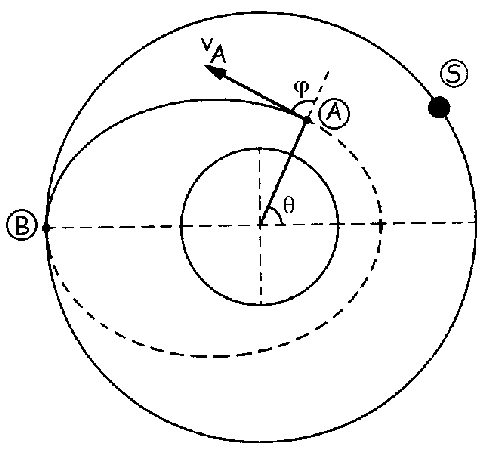
a) Llamaremos M a la masa de la Tierra, m a la del satélite y R al radio de la Tierra. El radio de la órbita circular en la que está el satélite es:

rS=hS+R=200+6370=6570 km

En dicha órbita circular, el satélite está sometido únicamente a la acción de la gravedad, y sólo tiene aceleración normal o centrípeta. Como fuerza y aceleración tienen la misma dirección y sentido, aplicando la segunda ley de Newton tendremos:

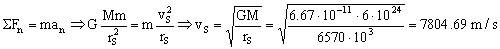
vS=7804.69 m/s

 

b) El tiempo que tarda en recorrer la órbita completa es el período. Para determinarlo aplicamos la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Tenemos entonces:

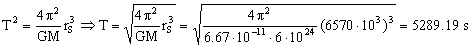
T=5289.19 s

 

c) La energía mínima para mantenerlo en esa órbita será la que tiene en cualquier instante, ya que la energía total es constante en toda la trayectoria, y el cambio de energía implica un cambio de órbita:

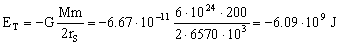
ET=-6.09 · 109 J

 

d) En el punto A conocemos tanto el radio como la velocidad:

rA=hA+R=100+6370=6470 km; vA=7882.9 m/s

Con estos dos parámetros podemos determinar la energía total en la órbita elíptica, que será:

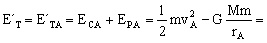
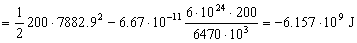
Como la energía total es constante, podemos aplicarla al punto B, y así determinar la velocidad que tiene el satélite en ese punto, ya que el radio es conocido:

rB=rS=6570 km

Tendremos entonces:

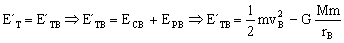
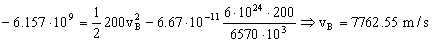
Ahora tenemos que también se mantiene constante el momento angular a lo largo de la trayectoria. Si aplicamos esta conservación entre los puntos A y B:

LA=LB ⇒ mrAvAsenφ=mrBvBsenφB

En el punto B el radio vector y la velocidad son perpendiculares, luego:

φB=90º ⇒ senφB=sen90º=1

Y nos queda:

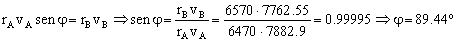
φ=89.44º

e) Para determinar el ángulo θ utilizaremos la ecuación de la trayectoria:

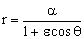
donde tendremos que calcular en primer lugar la ascensión recta y la excentricidad de la órbita. La ascensión recta puede calcularse a partir del momento angular:

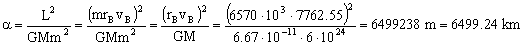
Nos queda la ecuación de la cónica:

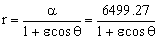
Además, conocemos un punto de la trayectoria, que es el punto B. Cuando r=rB ⇒ θ=180º ⇒ cosθ=-1 y tenemos:

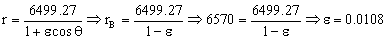
La ecuación de la trayectoria es entonces:

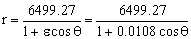
Ahora para el punto A tendremos que r=rA=6470 km:

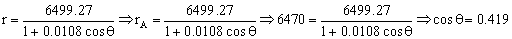
θ=65.23º