a) v=(5-4t)u_x+(10t²-4t³)u_θ
b) a=(-4-20t³+8t⁴)u_x+(30t-20t⁴)u_θ
c) F=188.68 dinas
d) r=2.12 cm

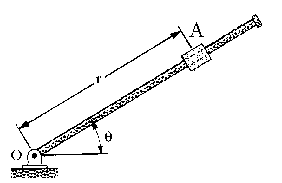
a) Si expresamos la velocidad del pasador en coordenadas polares planas tenemos:

u_r es un vector unitario en la dirección de r y u_θ un vector unitario perpendicular al anterior en sentido antihorario, como:

r=5t-2t² ⇒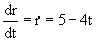

y como:

θ=t² ⇒

por tanto:

v=(5-4t)u_r+(10t²-4t³)u_θ

y el módulo de la velocidad:

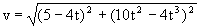
b) Para la aceleración en coordenadas polares tenemos:

;

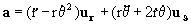
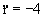Sustituyendo en la ecuación anterior tenemos:

a=(-4-20t³+8t⁴)u_r+(30t-20t²)u_θ

 

el módulo de la aceleración será:

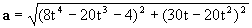
c) La fuerza que actúa sobre el pasador A es :

F=m_Aa

Como nos interesa en el instante en que t=1 s. Sustituimos en la expresión de la aceleración obtenida en el apartado anterior t por 1:

a=(-4-20t³+8t⁴)u_r+(30t-20t²)u_θ =-16u_r+10u_θ cm/s²

Por tanto:

F= 10 g (-16u_r+10u_θ) cm/s²= -160u_r+100u_θ dinas

El módulo de la fuerza será:

En el instante considerado, en que t=1s; r=5t-2t²=3 cm; θ=t²=1rad=57.29^º , tendremos el siguiente diagrama de fuerzas:

d) Para determinar el radio de curvatura de la trayectoria tendremos en cuenta que la aceleración normal ó centrípeta 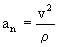siendo v el módulo de la velocidad de la partícula y r
el radio de curvatura de la trayectoria . Además la componente tangencial de la aceleración de la partícula . Si expresamos la aceleración en función de estas componentes (componentes intrínsecas) tenemos:

a=a_tu_t+a_nu_n;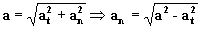

Del apartado c) tenemos:

del a):

y

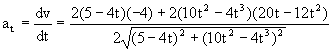
en el instante en que t=1 s, a_t= 7.23 cm/s² y

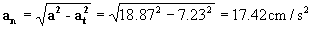
y por tanto: