Problema de Movimiento Oscilatorio

En el esquema de la figura se representa un resorte, en el interior de un tubo de paredes lisas, con uno de los extremos unido al extremo O del tubo y el otro a una masa m=100 g, que puede deslizar dentro del tubo. La constante elástica del resorte k=20 N/m, su longitud es de 10 cm y su masa despreciable. Hacemos girar el tubo, que está en un plano horizontal (XY), en torno a un eje perpendicular que pasa por O con velocidad angular constante ω=3 rad/s en sentido antihorario.
a) Calcular la deformación del resorte. b) Si desplazamos la masa desde la posición del apartado a) determinar la frecuencia angular de la oscilación resultante. c) Si el desplazamiento del apartado b) se realiza cuando el tubo pasa por la posición del eje X y es de 3cm determinar la posición de la masa cuando el tubo coincide con la dirección del eje Y.

a) Δl=0.47 cm
b) ω=13.82 rad/s
c) OP=12.23 cm

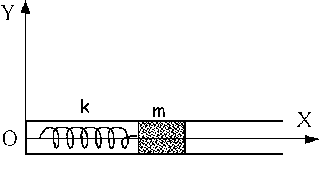
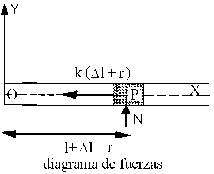
El mecanismo gira, en sentido antihorario con velocidad angular constante. Aislamos la partícula y trazamos el diagrama de sólido libre:

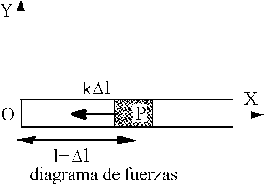
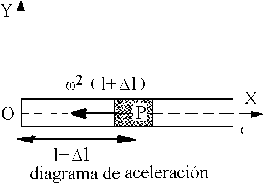
Aplicando la segunda ley de Newton tenemos:

F= m·a

F=-kΔl uOP+ Nun

Si ponemos la aceleración de la partícula en función del movimiento del tubo y de su movimiento relativo al tubo tenemos:

a=aO+αXOP+ωX(ωXOP)+2ωXvr+ar

Como O es un punto fijo aO=0, y como ω es constante α=0; por otra parte, en este caso tampoco existe movimiento relativo luego vr y ar son nulas:

a=ωX(ωXOP)=-ω2OP

Por tanto

-kΔl uOP+ Nun=m (-ω2OP) ⇒ -kΔl =-mω2OP y N=0

OP=l+Δl

sustituyendo en la ecuación anterior:

kΔl =mω2(l+Δl) ⇒ (k-mω2)Δl=mω2l ⇒

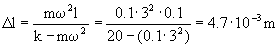
b) Si ahora desplazamos la partícula desde esa posición P a lo largo del tubo una longitud r hacia fuera si que hay movimiento relativo y por tanto vr y ar ya no son nulas.

Planteamos nuevamente las ecuaciones anteriores:

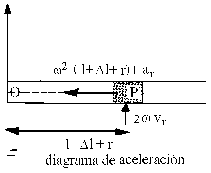
F= ma ⇒ -k(Δl+r) uOP´+ Nun=m (-ω2OP´+2ωXvr+ar) =

= m (-ω2 OP´uOP´+2ωuZXvr uOP´+ar uOP´)

Siendo uOP´, y un vectores unitarios (en el plano donde está situado el tubo , es decir el XY) en las direcciones de OP´y perpendicular a OP´ respectivamente. uZ vector unitario en dirección del eje z

-k(Δl+r) uOP´+ Nun=m(-ω2OP´uOP´+2ωvrun+ar uOP´)

Como OP´=l+Δl+r

-k(Δl+r)=m[-ω2(l+Δl+r)+ar] ⇒ -kΔl-kr+ mω2(l+Δl)+mω2r=ar

Como del apartado a) tenemos que: kΔl =mω2(l+Δl)

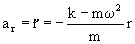
que corresponde a un movimiento armónico simple cuya frecuencia angular:

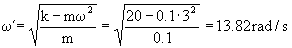
c) En el apartado anterior obtuvimos que el movimiento relativo de la partícula en el tuvo es un movimiento armónico simple cuya frecuencia angular es ω´=13.82 rad/s

El desplazamiento o elongación vendrá dado por la ecuación

r=Acosω´t

como la amplitud A=3 cm, si consideramos que es hacia fuera del tubo y empezando a contar en ese instante el tiempo, es decir cuando r=A:

r=3cos13.82t

Cuando haya transcurrido un tiempo igual al que tarda en girar el tubo un cuarto de vuelta (desde que coincide el tubo con la posición del eje X hasta que coincide con la posición del eje Y):

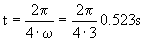
r=3cos (13.82 × 0.523) =1.76 cm

y la posición de la partícula con respecto a O ;

OP´= l+Δl+r=10+0.47+1.76 =12.23 cm

Podríamos haber desplazado la masa hacia dentro del tubo y en ese caso r=-3cos13.82t y la posición de la partícula sería en este supuesto

OP´= l+Δl+r=10+0.47-1.76=8.71 cm

También será una solución válida