Problema de Gravitación

Con el fin de reparar los paneles solares de un satélite terrestre, de comunicaciones, situado en una órbita geosíncrona (es decir permanece fijo respecto al suelo terrestre) se envía a unos técnicos en un vehículo espacial. Sabiendo que dicho vehículo describe inicialmente una órbita circular, coplanaria y en el mismo sentido que el satélite a 650 km sobre la superficie de la tierra, antes de pasar a la órbita elíptica de transición que le lleve hasta el satélite (ver figura). Determinar. a) El radio R de la órbita que describe el satélite así como su velocidad. b) El incremento de velocidad que deben de proporcionar los motores al vehículo en el punto A para transferirlo a la órbita elíptica de transición, así como el incremento de velocidad en B para acoplarse al satélite. c) El ángulo θ que define la posición del satélite, respecto al punto de encuentro, en el momento que el vehículo pasa a la trayectoria de transición .Masa de la tierra 6·1024 kg ; radio de la tierra 6370 km; constante de Gravitación universal G= 6.67·10-11 N·m2/kg2.

a) R=42228.664 km; v=3078.4 m/s
b) ΔvA=2337.2 m/s; ΔvB=1434.77 m/s
c) θ=80.21o

a) Como el satélite describe una órbita circular geosíncrona su velocidad angular es la velocidad angular de la tierra, por eso permanece fijo respecto al suelo terrestre.

Llamaremos M a la masa de la Tierra, R al radio de la órbita que describe el satélite y m a su masa. La única fuerza que actúa sobre el vehículo es la de atracción gravitatoria. Si aplicamos la segunda ley de Newton F=ma:

R=42228.664 km

La velocidad del satélite en la órbita v= ω·R=3078.4 m/s

v=3078.4 m/s

b) Vamos a determinar en primer lugar el incremento de velocidad del vehículo en el punto A, ΔvA, para pasar de la órbita circular a la elíptica de transición.

Inmediatamente antes del incremento de velocidad, el vehículo está en el punto A en la órbita circular de radio R1, y su velocidad es vA. Igual que en el caso anterior, la única fuerza que actúa sobre el vehículo es la de atracción gravitatoria, y la única aceleración es la normal o centrípeta, ya que el movimiento en esta órbita es circular y uniforme. Como tanto la fuerza como la aceleración tienen la misma dirección y sentido tendremos por aplicación de la segunda ley de Newton:

R1=(650+6370)× 103 m=7020000 m

Inmediatamente después del incremento de velocidad, la velocidad del vehículo será v´A, estará en el mismo punto A pero ya en la trayectoria elíptica. Para la trayectoria elíptica se conserva la energía luego:

La variación de velocidad en el punto A será la diferencia entre las velocidades después y antes del incremento:

Ahora pasamos al punto B y procedemos de modo análogo. Inmediatamente antes del incremento de velocidad, el vehículo estará en el punto B, su velocidad es vB y se encuentra en la órbita elíptica:

Inmediatamente después del incremento de velocidad, el vehículo está en ese mismo punto B, pero la velocidad es v´B y se encuentra en la órbita circular de radio R que habíamos determinado en el apartado a.

El incremento de velocidad es la diferencia entre las velocidades después y antes del incremento:

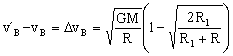
Si sustituimos los datos numéricos tendremos:

Y en el punto B tendremos:

c) El ángulo θ=ωt, siendo t el tiempo que tarda el satélite en barrer el ángulo θ que es el mismo tiempo que tarda el vehículo espacial en barrer medio elipsoide, teniendo en cuenta esto último t=T/2, siendo T el período de la órbita elíptica que podemos determinarlo aplicando la tercera ley de Kepler:

θ=ωt =7.29 10-5 (T/2)=1.4 rad = 80.21o