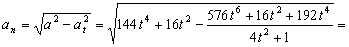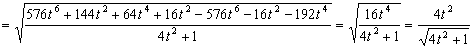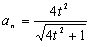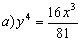
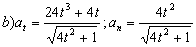
a) Las coordenadas x e y las obtenemos mediante integración de las componentes de la velocidad:
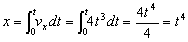
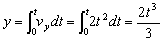
Ahora eliminaremos el tiempo entre estas dos ecuaciones:
x=t4
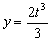
Elevamos la primera ecuación al cubo y la segunda a la cuarta:
x3=t12
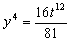
De la primera ecuación entonces:
t12=x3
Y sustituyendo en la segunda:
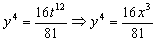
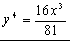
b) La aceleración es la derivada de la velocidad respecto del tiempo:
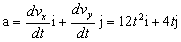
El módulo de la velocidad es:
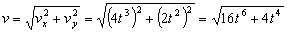
La aceleración tangencial es la derivada del módulo de la velocidad respecto del tiempo:
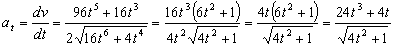
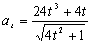
La aceleración normal podemos calcularla ya que sabemos la total:
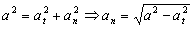
La aceleración al cuadrado es:
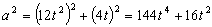
Y la aceleración tangencial al cuadrado:
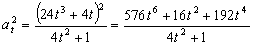
Por tanto la aceleración normal: