y=0.5cos(1.257t-0.126x)
La forma de la ecuación general es:
y=Asen(ωt± kx+φ0)
Como la onda se desplaza de izquierda a derecha, el signo correspondiente a la x es el negativo:
y=Asen(ωt-kx+φ0)
A partir de las condiciones iniciales:
t=0 ⇒ x=0 ⇒ y=A ⇒ A=Asenφ0 ⇒ senφ0=1 ⇒ φ0=π/2
Con lo cual nos queda la ecuación:
![]()
El desplazamiento máximo es la amplitud:
A=50 cm=0.5 m
El período serán 5 s, ya que ese es el tiempo que tarda la una partícula en pasar por el punto de máxima elongación dos veces consecutivas:
T=5 s
La distancia entre dos máximos es la longitud de onda, λ=50 m.
Y podemos calcular los dos parámetros que nos faltan, la frecuencia angular y el número de ondas:
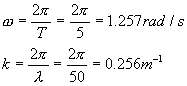
Sustituyendo obtenemos la ecuación de la onda:
y=Acos(ωt-kx)=0.5cos(1.257t-0.126x)
y=0.5cos(1.257t-0.126x)
con t en segundos y x e y en metros.