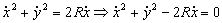a) v=R(1-cost)i+Rsentj; a=Rsenti+Rcostj;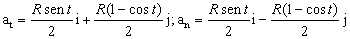

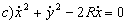
a) La velocidad es la derivada del espacio respecto del tiempo:

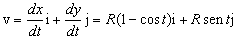
v=R(1-cost)i+Rsentj

Y la aceleración es la derivada de la velocidad respecto del tiempo:

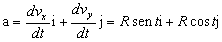
a=Rsenti+Rcostj

La aceleración tangencial es la derivada del módulo de la velocidad respecto del tiempo. El módulo de la velocidad es:

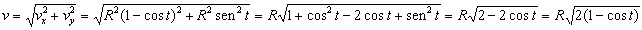
Entonces derivando:

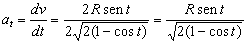
Si queremos la expresión vectorial de la aceleración tangencial, necesitaremos un vector unitario en dirección tangencial. Dicho vector podemos obtenerlo de la velocidad:

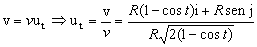
Entonces la aceleración tangencial como vector es:

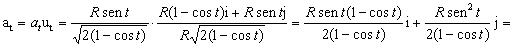
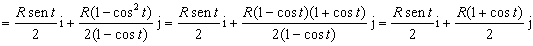
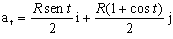
Para la aceleración normal tendremos:

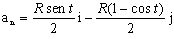
b) Para el radio de curvatura tenemos: el módulo de la aceleración normal

Su módulo es:

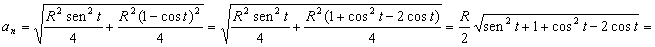
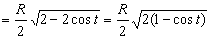
Y el módulo de la velocidad al cuadrado:

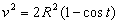
Entonces:

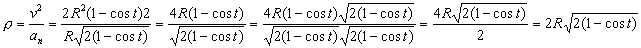
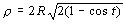
c) La trayectoria es la curva que describe el vector posición. La hodógrafa del movimientoes la curva que describe el vector velocidad. Por analogía, igual que para determinar la ecuación de la trayectoria eliminamos el tiempo entre las expresiones de x y de y, para determinar la hodógrafa tendremos que eliminar el tiempo entre las ecuaciones d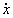e e 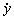. Las ecuaciones de las componentes de la velocidad son:

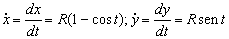
Si elevo las dos ecuaciones al cuadrado y las sumo tendré:

La ecuación de la hodógrafa es entonces: