b) e=1700 m; a=3.09 m/s 2 ; v=30.9 m/s
a) Durante 5 s el observador no nota nada, ya que ese es el tiempo que tarda el sonido en ir desde la locomotora hasta el observador.
A continuación y durante 10 s el tono del silbido se va haciendo más agudo. Como el observador está en reposo, eso significa que la fuente (locomotora) varía su velocidad, con lo cual varía la frecuencia percibida por el observador. Además, el tono se hace más agudo, es decir, la frecuencia percibida aumenta. Por efecto Doppler tendremos que la relación entre la frecuencia emitida y la percibida es:
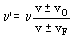
El observador está en reposo y la fuente se acerca luego:
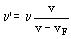
Si la frecuencia percibida aumenta el denominador de esa ecuación disminuye, y si el denominador disminuye es porque vF aumenta. Con esto deducimos que la velocidad de la locomotora aumenta, es decir, en ese intervalo está acelerando.
Por último, el tono del silbido permanece constante, lo que implica que vF se hace también constante, es decir, que a partir de aquí la locomotora continúa con movimiento rectilíneo y uniforme.
b) Sabemos que el sonido tarda 5 s en llegar desde la locomotora hasta el observador. El sonido se propaga con velocidad uniforme, luego tendremos:
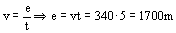
e=1700 m
La frecuencia real emitida por la fuente es:
ν=300 s-1
Y la percibida por el observador al final:
ν’=330 s-1
Aplicando la fórmula del efecto Doppler en esta posición tendremos:
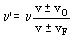
Si tenemos en cuenta que el observador está en reposo y la fuente se acerca:
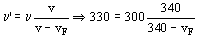
De donde obtenemos la velocidad final de la locomotora:
vF=30.91 m/s
Ahora conocemos la velocidad final de la locomotora, la inicial (parte del reposo) y el tiempo durante el cual el movimiento es rectilíneo y uniforme. Aplicando la fórmula correspondiente:
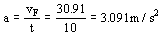
a=3.091 m/s2