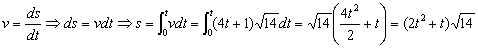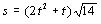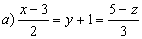
b) v=(2+8t)i+(1+4t)j+(-3-12t)k; v0=2i+j-3k; vm=18i+9j-27k
c) a=8i+4j-12k; an=0 ; 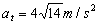
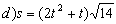
a) Tenemos las ecuaciones:
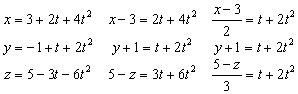
Como los segundos miembros son iguales, los primeros también lo serán, y nos queda que la trayectoria viene dada por la ecuación:
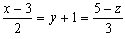
b) La velocidad instantánea será la derivada de la velocidad respecto del tiempo:
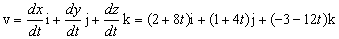
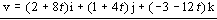
La velocidad inicial es la velocidad cuando t=0:
v0=2i+j-3k
El vector de posición es:
r=xi+yj+zk=(3+2t+4t2)i+(-1+t+2t2)j+(5-3t-6t2)k
Entonces para t=1 s:
r1=( 3+2+4)i+(-1+1+2)j+(5-3-6)k=9i+2j-4k
Y para t=3 s:
r3=( 3+2·3+4·32)i+(-1+3+2·32)j+(5-3·3-6·32)k=45i+20j-58k
La velocidad media será entonces el incremento de la posición partido por el incremento de tiempos, es decir:
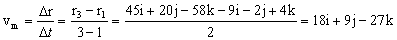
vm=18i+9j-27k
c) La aceleración será la derivada de la velocidad respecto del tiempo:

a=8i+4j-12k
Como la trayectoria es una recta (ver la ecuación) la aceleración normal será nula (ya que el radio de curvatura sería infinito):
an=0
Y la aceleración por tanto sólo tendría componente tangencial:
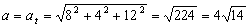
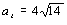
Podría ocurrir que uno no se diera cuenta de que la ecuación de la trayectoria es la ecuación de una recta, con lo que no deduciría que la aceleración normal es nula. En este caso, como en los demás problemas, podemos calcular en primer lugar la aceleración tangencial, que es la derivada del módulo de la velocidad respecto del tiempo. El módulo de la velocidad es:
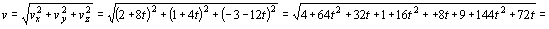
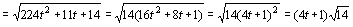
Y tendremos que la aceleración tangencial es:
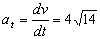

Y para la normal:
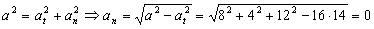
an=0
d) Tenemos calculado el módulo de la velocidad que es:
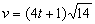
Por tanto tendremos que el espacio será: