416.89 Hz < ν´< 465.83 Hz
En primer lugar pasamos la velocidad angular a radianes por segundo:
ω=30 r. p. s.=188.5 rad/s
Ahora tenemos que el movimiento es circular uniforme, luego la fuente, a la que denotaremos con la letra S, tendrá una velocidad lineal que será la angular por el radio:
vS=ωr=188.5·0.1=18.85 m/s
En la fórmula del efecto Doppler tendremos:
![]()
Como el observador está en reposo:
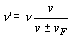
Además tenemos que proyectar las velocidades sobre la recta de unión observador-fuente. Dependiendo de dónde se encuentre la fuente, tendremos que su velocidad (tangente a la circunferencia en el punto dado) formará un cierto ángulo con la recta que une el observador con la fuente. Tendremos entonces al proyectar:
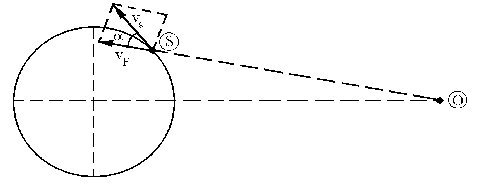
vF=vScosα
Y en la ecuación del efecto Doppler me quedará:
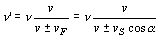
Es obvio que para que la frecuencia percibida sea máxima el denominador de esa ecuación debe ser mínimo. Ese denominador será lo más pequeño posible cuando tenga el signo negativo (la fuente estaría acercándose al observador) y además el cosα tome su valor máximo, es decir la unidad. En este caso el ángulo a será nulo, lo que significa que la recta que une el observador con la fuente coincide con la dirección de la velocidad, o sea, la recta observador-fuente es tangente a la circunferencia.
De modo análogo, para que la frecuencia percibida sea mínima, el denominador de la ecuación debe ser máximo, por lo que el signo que debe aparecer es el positivo (la fuente se aleja del observador), y además, el cosa también será igual a la unidad. Tendremos entonces los puntos que se marcan en el dibujo señalados como puntos M y m, donde la frecuencia percibida será máxima y mínima respectivamente.
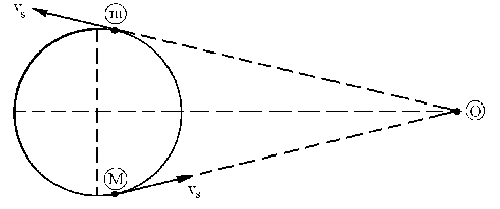
Para la frecuencia máxima, teniendo en cuenta todo lo explicado anteriormente tendremos:
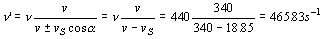
Y para la frecuencia mínima:
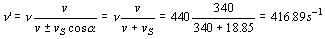
Tendremos entonces el intervalo de frecuencias:
465.83 s-1< ν’ <416.89 s-1