Una barra rígida de 1 m de longitud, cuyo peso -

Problema de Propiedades Elásticas de los Sólidos

Una barra rígida de 1 m de longitud, cuyo peso es despreciable, está sostenida horizontalmente en sus extremos por dos hilos verticales de la misma longitud; uno de ellos es de acero y el otro de cobre, tal como su muestra en la figura adjunta, siendo sus respectivas secciones rectas de 1 mm² y 2 mm² respectivamente. ¿En qué punto de la barra ha de suspenderse un peso W para producir: a) igual esfuerzo en ambos hilos? b) igual deformación unitaria en ambos hilos? E_Cu=12.8·10¹⁰ N/m²; E_A=20·10¹⁰ N/m².

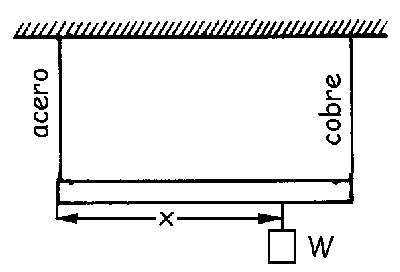
a) x=0.667 m
b) x=0.561 m

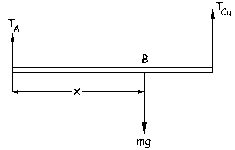a) En principio suponemos que la barra permanece siempre en posición horizontal. Trazamos el diagrama de sólido libre de la barra, que será el que aparece en la figura. El sistema está en equilibrio, luego si tomamos como eje Y al eje vertical tendremos:

ΣF_y=0 ⇒ T_A+T_Cu-W=0 ⇒ T_A+T_Cu=W

Además, como la barra no rota:

ΣM_A=0 ⇒ T_Cu·1-Wx=0 ⇒ T_Cu=Wx

Además, como las deformaciones unitarias son iguales:

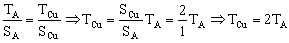
Tenemos entonces el sistema de tres ecuaciones:

T_A+T_Cu=W

T_Cu=Wx

T_Cu=2T_A

Sustituimos la tercera ecuación en las otras dos:

T_A+T_Cu=W ⇒ T_A+2T_A=W ⇒ 3T_A=W

T_Cu=Wx ⇒ 2T_A=Wx

Y ahora sustituimos la primera ecuación en la segunda:

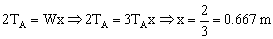
x=0.667 m

b) A partir del módulo de Young tenemos:

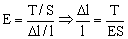
Como la deformación unitaria debe ser igual:

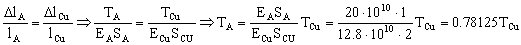
Tenemos además las mismas ecuaciones de fuerzas y momentos que en el apartado anterior, luego nos queda el sistema de ecuaciones:

T_A+T_Cu=W

T_Cu=Wx

T_A=0.78125T_Cu

Sustituimos la tercera expresión en las anteriores:

T_A+T_Cu=W ⇒ 0.78125T_Cu+T_Cu=W ⇒ 1.78125T_Cu=W

T_Cu=Wx ⇒ T_Cu=Wx

Y sustituyendo la primera expresión en la segunda:

T_Cu=Wx ⇒ T_Cu=1.78125T_Cux ⇒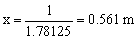

x=0.561 m