a) W=52.59 N
b) Δl_A=0.54 mm; Δl_Cu=1.46 mm
c) (E_Pe)_A=0.0143 J; (E_Pe)_Cu=0.383 J
d) E=1.31·10¹¹ N/m²

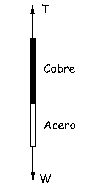a) En primer lugar aislamos el sistema de dos hilos, con lo que tendremos lo que aparece en la figura. El sistema está en equilibrio, por lo que si tomamos como eje Y el eje vertical tendremos:

ΣF_y=0 ⇒ T-W=0 ⇒ T=W

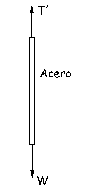Ahora vamos a aislar cada uno de los hilos por separado. Para el hilo de acero, que también está en equilibrio:

ΣF_y=0 ⇒ T´-W=0 ⇒ T´=W

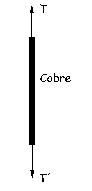Y por último, para el hilo de cobre:

ΣF_y=0 ⇒ T-T´=0 ⇒ T=T´

Como podemos ver, todos los cables soportan la misma tensión que es igual al peso W. Ahora vamos a pasar todo al Sistema Internacional:

l_Cu=3 m; l_A=2 m; S_Cu=S_A=1 mm²=10^-6 m²; E_Cu=1.1 · 10⁴ kp/mm²=1.078 · 10¹¹ N/m²;

E_A=2 · 10⁴ kp/mm²=1.96 · 10¹¹ N/m²; Δl=2 mm=2 · 10^-3 mm

Ahora tendremos que para el cobre:

Y para el acero:

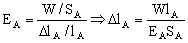
Sabemos que:

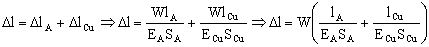
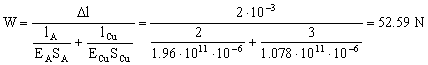
Y si queremos la masa en vez del peso:

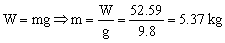
m=5.37 kg

 

b) Ahora sustituimos en las expresiones de las variaciones de longitud:

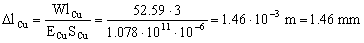
Δl_Cu=1.46 mm

Y para el otro:

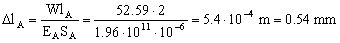
Δl_A=0.54 mm

También podríamos haber determinado este alargamiento teniendo en cuenta que entre los dos deben sumar 2 mm:

Δl=Δl_A+Δl_Cu ⇒ Δl_A=Δl-Δl_Cu=2-1.46=0.54 mm

c) Para el cobre la energía elástica almacenada es:

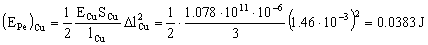
(E_Pe)_Cu=0.0383 J

Y para el acero:

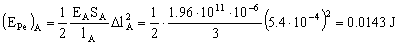
(E_Pe)_A=0.0143 J

d) Para tener un único hilo que sea equivalente a los dos anteriores deberá tener la misma sección:

S=10^-6 m²

Su longitud será suma de las dos longitudes anteriores:

l=l_A+l_Cu=2+3=5 m

Y además, bajo el mismo peso de 52.59 N deberá alargarse:

Δl=Δl_A+Δl_Cu=2 mm=2·10^-3 m

El módulo de Young será entonces:

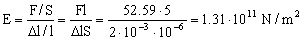
E=1.31·10¹¹ N/m²