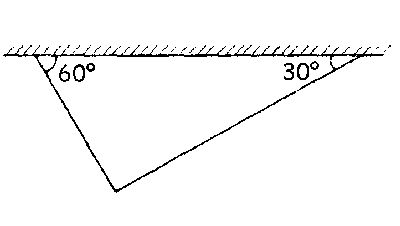
a) el de hierro se romperá antes
b) Δl_Cu=8.18·10^-4 m; Δl_Fe=2.25·10^-3 m

a) Pasamos todo al Sistema Internacional:

S_Cu=5 mm²=5·10^-6 m²; S_Fe=2 mm²=2·10^-6 mm²;

E_Cu=11·10³ kg/mm²=1.078 · 10¹¹ N/m²; E_Fe=10⁴ kg/mm²=9.8·10¹⁰ N/m²;

σ_Rcu=30 kg/mm²=2.94·10⁸ N/m²; σ_Rfe=40 kg/mm²=3.92·10⁸ N/m²

 

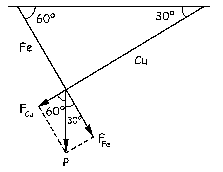Ahora descomponemos el peso P que cuelga de la anilla en sus componentes según las direcciones de los alambres, para ver la fuerza que soporta el alambre de cobre y la fuerza que soporta el alambre de hierro. La fuerza que soporta cada alambre es:

F_Cu=Pcos60º; F_Fe=Pcos30º

Para que se rompa el alambre de cobre habrá que colgar un peso P tal que el esfuerzo que soporte dicho alambre sea igual a la tensión de rotura, es decir:

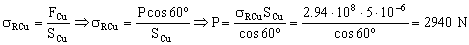
Para que se rompa el alambre de hierro habrá que colgar un peso P tal que el esfuerzo que soporte dicho alambre sea igual a la tensión de rotura:

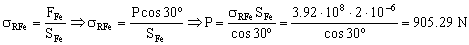
El hierro rompe cuando se cuelga un peso P de 905.29 N, mientras que el cobre rompe cuando se cuelga un peso P de 2940 N. Rompe por tanto antes el alambre de hierro.

ROMPE PRIMERO EL HIERRO

 

b) Si colgamos un peso de 30 kg tendremos:

P=mg=30 · 9.8=294 N

Como este peso es menor a los 905.29 N con los que rompe el hierro, no rompería ninguno de los dos alambres, sino que ambos se estirarían.

Las fuerzas que soportan cada uno de los dos alambres son:

F_Cu=Pcos60º=294cos60º=147 N; F_Fe=Pcos30º=294cos30º=254.61 N

Para el cobre entonces tendremos:

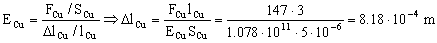
Δl_Cu=8.18 · 10^-4 m

Para el hierro primero tenemos que hallar su longitud. A través del teorema del seno:

Por tanto para el hierro:

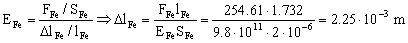
Δl_Fe=2.25·10^-3 m