Problema de Propiedades Elásticas de los Sólidos

Un hilo de acero de 1 m de longitud y 1 mm2 de sección recta está extendido horizontalmente entre dos soportes rígidos unidos a sus extremos. Entonces, se cuelga un peso de 5 kg del punto medio del hilo. a) Calcular el descenso que experimenta el punto medio del hilo, así como el esfuerzo tensor que soporta el mismo; b) calcular la energía elástica almacenada en el hilo tensado. Módulo de Young del acero: E=20·1010 N/m2

a) Δy=3.13 cm; σ=3.92·108 N/m2
b) EPe=0.383 J

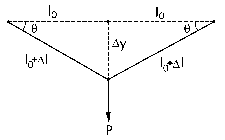
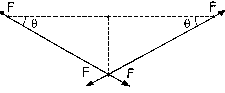
a) El hilo quedará al colgar el peso tal como se muestra en la figura. Denominaremos eje Y al eje vertical. Por el teorema de Pitágoras tendremos:

Δy2=(l0+Δl)2-l02=l02+Δl2+2l0Δl-l02=Δl2+2l0Δl

Despreciamos los infinitésimos de orden 2 y superiores y nos queda:

Δy2=Δl2+2l0Δl >> 2l0Δl ⇒ Δy2=2l0Δl

siendo l0:

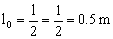
La variación de longitud Δl podemos obtenerla a partir del módulo de Young:

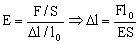
donde F es la fuerza en la dirección del cable.

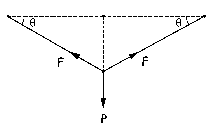Si aislamos el peso, teniendo en cuenta la simetría, tendremos lo que aparece en la figura. El peso está en equilibrio por lo que se cumplirá que:

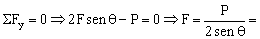
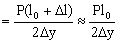
Para el cable:

Sustituyendolo en la expresión de Δl tendremos:

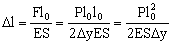
Y sustituyendo en la expresión de Δy:

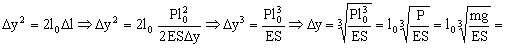
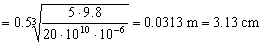
Δy=3.13 cm

La fuerza F que soporta el hilo es:

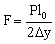
Por tanto el esfuerzo (fuerza por unidad de área):

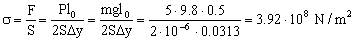
σ=3.92 · 108 N/m2

 

b) La energía potencial elástica es:

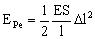
La variación de longitud la podemos obtener del módulo de Young:

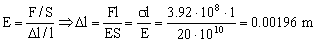
Entonces:

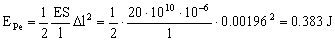
EPe=0.383 J